Sketching graphs in polar coordinates

[shamieh]

I don't understand why I am screwing this up so bad.

Sketch the graph of the equation $$r = 2 + 4cos(\theta)$$ in polar coordinates.

So I did:

$$0 = 2 + 4cos(\theta) $$
$$= -\frac{1}{2} = cos(\theta)$$

Then got $$cos(\theta)$$ is $$-\frac{1}{2}$$ @ $$\frac{2\pi}{3}$$ and @$$ \frac{4\pi}{3} $$

Then i plotted points to get

0 ,6
pi/2 , 2
pi, -2
3pi/2 , 2
2pi, 6

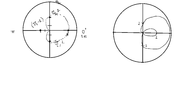
And I'm not understanding where they are getting the 2 for the like inner loop part of the centroid... My graph is on the left... The one on the right is what its supposed to look like.

View attachment 2134

I'm getting everything the same except I'm not getting the inner loop

 

[MarkFL]

A radius of -2 at the angle of $\pi$ would be at the Cartesian point (2,0)...do you see why?

 

[shamieh]

A radius of -2 at the angle of $\pi$ would be at the Cartesian point (2,0)...do you see why?

No I don't actually. Why is that? I mean I know that it should be (2,0) I just don't understand the logic behind it or why, but I know it obviously is because I'm getting the wrong graph lol.

 

[MarkFL]

The polar point $(r,\pi)$ will lie along the $x$-axis. If $r$ is positive, then the point is on the negative $x$-axis and if $r$ is negative, the point will be on the positive $x$-axis. Think of the rectangular translation for this point:

$$x=r\cos(\pi)=-r$$

$$y=r\sin(\pi)=0$$

Hence, the polar point:

$$(r,\pi)$$

is the rectangular point:

$$(-r,0)$$