Snell's Law: Definition, Equations, Refractive Index & Critical Angle

[Greg Bernhardt]

Definition/Summary

Snell's Law relates the angles of incidence and refraction, for a light ray that passes between two media of different refractive indices.

The refractive index of a medium is the speed of light in vacuum divided by the speed of light in the medium: n = c/v. It is the "optical density" of the medium. It is always greater than 1, as long as there is a physical medium other than vacuum.

Equations

Snell's law:

n_1 \ \sin \theta_1 <br /> \ = \ n_2 \ \sin \theta_2


or equivalently:

<br /> \frac{\sin \theta_1}{\sin \theta_2} <br /> \ =\ \frac{n_2}{n_1}<br /> \ =\ \frac{v_1}{v_2}<br />


Critical angle for total internal reflection:

\sin\theta_c\ =\ \frac{n_2}{n_1}


Refractive index:

n\ =\ \frac{c}{v}


Typical refractive indices:

Vacuum: n = 1 exactly
Air: n = 1.0003, often approximated by 1
Water: n = 1.34, average over visible range
Glass: n = 1.5 is typically used in optics homework problems
Fused silica (pure SiO2 glass): n = 1.46, average over visible range

For a comprehensive list, see http://en.wikipedia.org/wiki/List_of_refractive_indices

Extended explanation

Definitions of terms:

n₁, n₂ are the refractive indices for the two media.

θ₁, θ₂ are the angles that the rays make, with respect to the normal, for each medium. Usually θ₁ is taken as the angle of incidence, and θ₂ is the angle of refraction; however this distinction is unimportant due to the symmetry of Snell's Law.


Illustrative figure

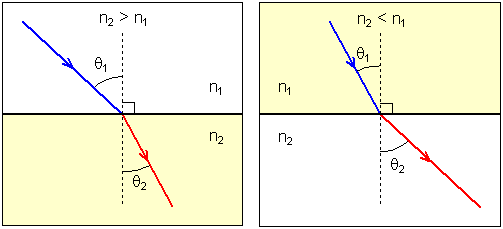For n₂ > n₁, the ray bends towards the normal upon refraction at the interface.
For n₂ < n₁, the ray bends away from the normal.


Total internal reflection:

Snell's law requires that light bends towards the surface (away from the normal) on passing from a denser medium to a less dense medium. So there is a critical angle of incidence, θ_c, at which light would bend so much that it would skim the surface; at any greater angle of incidence, Snell's law does not allow an angle of refraction, and so the light is completely reflected back into the denser medium.


Dependence on wavelength (dispersion):

The speed of light (and therefore the refractive index) in a medium generally depends on wavelength, and light of different wavelengths will be refracted at different angles.


Chromatic aberration:

And so light of mixed wavelengths (such as sunlight) will spread out (disperse) into its component colours.

In optical instruments, this dispersion causes light of different wavelengths to focus at different points. This blurring of the image is called chromatic aberration.


Dependence on direction (anisotropy):

In some media, the speed of light depends on the direction through the medium and on the polarisation of the light.

* This entry is from our old Library feature. If you know who wrote it, please let us know so we can attribute a writer. Thanks!

 

[APhysicist]

Snell's Law is a mathematical equation that relates the angles of incidence and refraction of a light ray passing between two media with different refractive indices. The refractive index is the "optical density" of medium, which is always greater than 1 as long as there is a physical medium other than vacuum. The equation is expressed as n_1*sin(theta_1) = n_2*sin(theta_2). There is also a critical angle for total internal reflection, which occurs when n_2/n_1 is equal to the sine of the critical angle. The refractive index of common materials such as vacuum, air, water, glass, and fused silica can be found online. Additionally, the speed of light in a medium can vary depending on the wavelength and direction of the light, which can cause chromatic aberration in optical instruments.