Solid disk rolling down an inclined plane -- Some conceptual questions

[LCSphysicist]

Homework Statement

Actually is a conceptual doubt

Relevant Equations

L = Iw
T = rf
g = g

I was always a little confused about the rolling down of a body, let's say, a sphere.
It's know that to body rotate, from the rest, in a referential frame on the ground [inertial], is necessary a friction, that will just act like a medium that transforms kinetic energy of translation into rotation.

I want to justify this, because if we take a torque about the point of contact, will the weight the producing force of such, and this can make a confusion i guess. I will try justify to myself to clarify the ideas and would like that you help me.

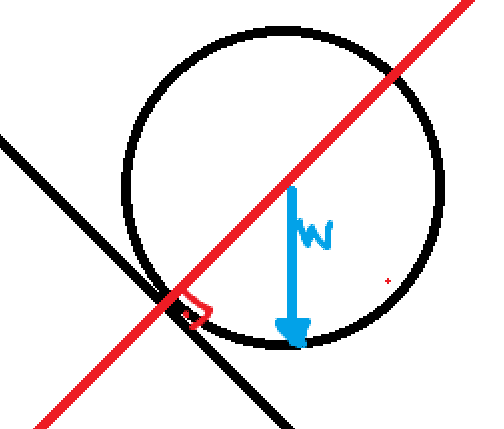
So about the contact point, the weight will produce a torque T = (-rmgsiny)k^. We know too that the angular momentum about that point is (-Ip*w)k, Ip relative to this point [not to center of mass]

But, T = L', so

-r*m*g*siny = -Ip*a(alpha)

Well, the point is, w is not constant, this is where i think that confused me, i need to clarify once and for all this point.

a is not constant RELATIVE to the point, it doesn't the same thing to say that the body will rotate, since we know that the instantaneous w of a point is equal to v/d (d relative a point), if the v varies, w will to, not about rotation ordinary.

Now, analyzing by the center of mass, we have L = Io*w, if w is constant we could stop, assume that w varies.
So L will varies to, but, if we analyze all the forces in the body, immediately we could say:
There is a Normal, and a Weight force, passing the center that produce no torque.

Assuming the resistive force of the air nonexist, and the body as rigid, the only force here to make it varies is the friction.

Now we know that the friction produce the torque, so route about the center of mass, which is the only relative motion possible to a particle on the body.
That's the "true" rotation that we always says.

Is this right?

 

[haruspex]

alpha is not constant RELATIVE to the point

Not sure if this answers your question, but you do need to be careful about choice of axis in rotational acceleration. Here, what do you mean by "the point"?
If you mean the fixed point on the ramp which happens to be the instantaneous point of contact then alpha is constant and you should run into no difficulties. But if you mean the point of the disc which happens to be the instantaneous point of contact then that is not inertial and can lead you astray.
Note that taking the mass centre as (a moving) axis does work even though it is non-inertial.

 

[LCSphysicist]

Not sure if this answers your question, but you do need to be careful about choice of axis in rotational acceleration. Here, what do you mean by "the point"?
If you mean the fixed point on the ramp which happens to be the instantaneous point of contact then alpha is constant and you should run into no difficulties. But if you mean the point of the disc which happens to be the instantaneous point of contact then that is not inertial and can lead you astray.
Note that taking the mass centre as (a moving) axis does work even though it is non-inertial.

Oh no, it's about the instantaneous point of contact :Z, i really forget that it is not an inertial reference frame... Okay, now i really in doubt how to justify this things with mathematic.
The question is, yeh got a little confused but, justify that the weight torque don't make the disk/spere whatever rotate by itself, what can seem contradictory to someone starting the study of rotation and solid (someone = me).

 

[LCSphysicist]

I am trying to justify (with math) to my intuition why the weight torque don't make the body spin.

 

[haruspex]

I am trying to justify (with math) to my intuition why the weight torque don't make the body spin.

But it does, if you choose the point of the ramp in contact with the sphere as axis.
With that axis:
Torque = $-mgr\sin(\theta)$
MoI = $I_c+mr^2$
$\alpha= -\frac{mgr\sin(\theta)}{I_c+mr^2}$
Starting again, with mass centre as axis:
$-mr\alpha=ma=mg\sin(\theta)-F_{fric}$
$I_c\alpha=-rF_{fric}=-mr^2\alpha-mgr\sin(\theta)$
Which leads to the same result.

 

[LCSphysicist]

But it does, if you choose the point of the ramp in contact with the sphere as axis.
With that axis:
Torque = $-mgr\sin(\theta)$
MoI = $I_c+mr^2$
$\alpha= -\frac{mgr\sin(\theta)}{I_c+mr^2}$
Starting again, with mass centre as axis:
$-mr\alpha=ma=mg\sin(\theta)-F_{fric}$
$I_c\alpha=-rF_{fric}=-mr^2\alpha-mgr\sin(\theta)$
Which leads to the same result.

But is not necessary a friction to make the body spin?
Oh... Maybe i am confused because, please correct if I'm wrong, have two types the body spin.
One with slipping and other without slipping, the friction is necessary to the latter, but is not necessary to make just the body spin!?

 

[LCSphysicist]

What you think about this text?

Let's consider a body of circular section (ring,
cylinder, ball) rolling without sliding on a plane
inclined angle 0 and height h (Fig.12.24). Prune
take the strength-weight Mg as applied in the center of
mass C (pg. 259). Soon, neither this FORCE nor the reaction
N of the plane exert a torque relative to the
CM, capable of producing rotation. If they were only
these are the acting forces, the body would slide
the plan. In order for there to be bearing, it is necessary that we take into account the friction: the friction force F, applied at the point of contact Po (figure), exerts a torque F relative to the Center C (R = radius of the section). In the case of pure bearing, Po belongs to the instantaneous axis of rotation, so it is at rest every instant. So, F. is the static friction force (in reality, instead of a point of contact, there is a small area a Depression of the plane, which leads to the so-called bearing friction, but we will not consider this effect).

Moyses vol one.

 

[haruspex]

But is not necessary a friction to make the body spin?
Oh... Maybe i am confused because, please correct if I'm wrong, have two types the body spin.
One with slipping and other without slipping, the friction is necessary to the latter, but is not necessary to make just the body spin!?

The equation MoI = $I_c+mr^2$ assumed the point of contact is the axis of rotation. If no friction then the torque about the instantaneous point of contact is still $-mgr\sin(\theta)$, but the MoI to use is now just mr². This gives an angular acceleration $-\frac gr\sin(\theta)$. That is correct: the linear acceleration $g\sin(\theta)$, viewed from a fixed point on the ramp, constitutes an angular acceleration $-\frac gr\sin(\theta)$.

The text in post #7 looks fine. Without friction it will not rotate.

 

[LCSphysicist]

The equation MoI = $I_c+mr^2$ assumed the point of contact is the axis of rotation. If no friction then the torque about the instantaneous point of contact is still $-mgr\sin(\theta)$, but the MoI to use is now just mr². This gives an angular acceleration $-\frac gr\sin(\theta)$. That is correct: the linear acceleration $g\sin(\theta)$, viewed from a fixed point on the ramp, constitutes an angular acceleration $-\frac gr\sin(\theta)$.

The text in post #7 looks fine. Without friction it will not rotate.

Ohh so here were my problem, looking a torque without friction i thought that it would have angular acceleration, indeed it has, the problem is that i didn't noticed that the angular acceleration it not an spin acceleration about CoM, is about a point on the ramp>:O

thx

 

[haruspex]

Ohh so here were my problem, looking a torque without friction i thought that it would have angular acceleration, indeed it has, the problem is that i didn't noticed that the angular acceleration it not an spin acceleration about CoM, is about a point on the ramp>:O

thx

That's it!