- #1
saruji
- 3
- 0
The file is a PDF, but here is an imgur link, anyone?
Solid of solids, pretty sure I got the wrong answer, not sure what I did wrong.
In summary, the conversation discusses the correct setup for an integral involving horizontal disks and the use of shells instead of washers. It is recommended to use two integrals, one from 0 to 1/2 and the other from 1/2 to 1, to find the total area. The previous incorrect integral is also mentioned.
- #2
Mark44
Mentor
- 37,743
- 10,085
That is incorrect, because your integral is not set up correctly. You are using horizontal disks (washers), but because of the shape of the region, their formula needs to change at y = 1/2. Between 0 and 1/2, the washers have the same outside diameter. Between 1/2 and 1, the washers have a different outside diameter. Since the formulas are different, you will need two integrals.saruji said:The file is a PDF, but here is an imgur link, anyone?
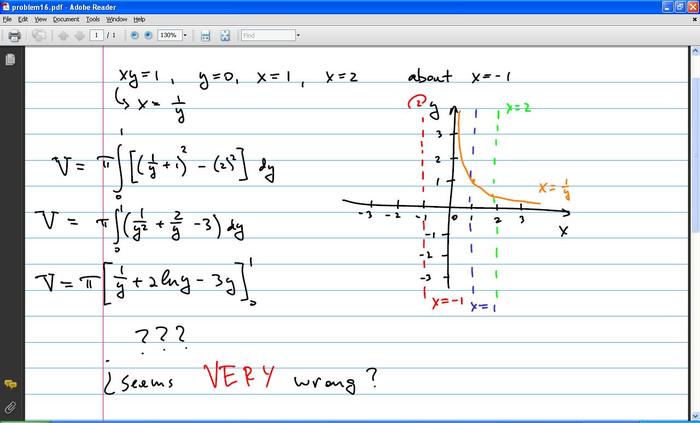
I would probably be inclined to use shells rather than washers in this problem.
- #3
saruji
- 3
- 0
So what would be my limits of integration than?...Having a hard time picturing this for some reason...
- #4
iRaid
- 559
- 8
Lol, I had this exact same problem on my quiz last week and got it wrong. I figured it out after class (while driving home, unfortunately) and what you have to do is set up 2 integrals. One from 0 to 1/2 and the other from 1/2 to 1. Adding these together gives you the total area.
[tex]\pi\int_0^.5 (outer)^{2}-(inner)^{2} dy + \pi\int_.5^1 (outer)^{2}-(inner)^{2} dy[/tex]
That should make it much easier.
Edit: Just to add, you can tell yours is wrong when you go to evaluate it, what's ln 0? undefined..
[tex]\pi\int_0^.5 (outer)^{2}-(inner)^{2} dy + \pi\int_.5^1 (outer)^{2}-(inner)^{2} dy[/tex]
That should make it much easier.
Edit: Just to add, you can tell yours is wrong when you go to evaluate it, what's ln 0? undefined..
Last edited:
- #5
saruji
- 3
- 0
iRaid said:
Thank you so much
FAQ: Solid of solids, pretty sure I got the wrong answer, not sure what I did wrong.
What is a solid of solids?
A solid of solids is a geometric shape formed by combining multiple solid shapes, such as cubes, spheres, and cylinders, into one larger solid shape.
How do you calculate the volume of a solid of solids?
The volume of a solid of solids can be calculated by finding the volume of each individual solid shape and then adding them together.
What is the difference between a solid of solids and a composite solid?
A solid of solids is a specific type of composite solid where the individual shapes are combined to create one larger shape. A composite solid can refer to any combination of solid shapes.
What is the formula for finding the surface area of a solid of solids?
The formula for finding the surface area of a solid of solids depends on the specific shapes that make up the solid. Generally, the surface area can be found by adding the surface areas of each individual shape.
Can a solid of solids have curved edges?
Yes, a solid of solids can have curved edges if the individual shapes that make up the solid have curved edges. For example, a solid of solids made up of spheres and cylinders can have curved edges.