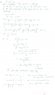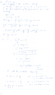PcumP_Ravenclaw
- 105
- 4
Homework Statement
Solve the equation ## z^3 + 6z = 20 ## (this was considered by Cardan in Ars
magna).
Homework Equations
Please see the 2nd attachement.
The Attempt at a Solution
I want to know if my solution is correct because the book (2nd attachment) says that there should only be 3 distinct solutions. I get 4 distinct solutions. My method is also slightly different from the book because I don't understand v and v1 etc...
Please explain to me how to solve cubic equations by the method explained in this attachment only. I don't want to solve this by euler's or any other method.
For my attempt please see the 1st attachment
Danke...