gastro54
- 3
- 0
Homework Statement
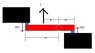
Figure is an overhead view of a rigid rod that turns about a vertical axle until the identical rubber stoppers A and B are forced against the rigid walls at distances rA = 7cm, rB = 4cm. Initially, the stoppers touch the walls without being compressed. Then force F of magnitude 220N is applied perpendicular to the rod at a distance R = 5cm. Find the magnitude of the force compressing stopper A and stopper B.
Homework Equations
I'm not sure how elasticity even plays into this problem... Should I treat this as an equilibrium type problem?
F = (+) FN1 = (-) FN2 = (+)
R = (-) rA = (-) rB = (+)
Tnet = 0, Fnet = 0
T1 = RF
T2 = rB(FN2)
T3 = rA(FN1)
T1 + T2 + T3 = 0
RF + rB(FN2) + rA(FN1) = 0
F + FN1 + FN2 = 0
The Attempt at a Solution
Not sure where to start really...
Diagram:
http://img90.imageshack.us/img90/3256/elasticityvt0.jpg
Attachments
Last edited by a moderator: