mathlearn
- 331
- 0
(Sweating) Any Ideas on how to begin?
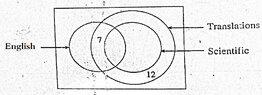
An incomplete Venn diagram containing the information about 100 types of books displayed at bookstall is shown in the figure.
View attachment 5975
(i) There were 70 translation book types and also there were 40 scientific translation book types that were not in English. How many English scientific translation book types were there?
(ii) If there were 20 English book types, how many of them were not translations?
(iii) Show that the number of book types which were neither in English nor translations were $\frac{7}{25}$ of the total number of types displayed in the bookstall.
(iv) Taking into account the selling ratios of book types he had experienced during the previous sales the bookstall owner had brought the book types to the stall in the same ratio. Find the probability that a randomly chosen student who visited the bookstall had bought an English translation book type.
Many Thanks :)
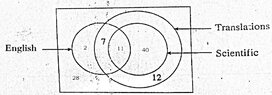
An incomplete Venn diagram containing the information about 100 types of books displayed at bookstall is shown in the figure.
View attachment 5975
(i) There were 70 translation book types and also there were 40 scientific translation book types that were not in English. How many English scientific translation book types were there?
(ii) If there were 20 English book types, how many of them were not translations?
(iii) Show that the number of book types which were neither in English nor translations were $\frac{7}{25}$ of the total number of types displayed in the bookstall.
(iv) Taking into account the selling ratios of book types he had experienced during the previous sales the bookstall owner had brought the book types to the stall in the same ratio. Find the probability that a randomly chosen student who visited the bookstall had bought an English translation book type.
Many Thanks :)
Attachments
Last edited: