chwala
Gold Member
- 2,828
- 421
- Homework Statement
- see attached
- Relevant Equations
- variance
The question is below:
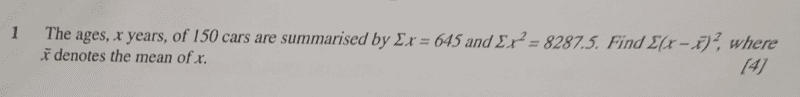
below is my own working;
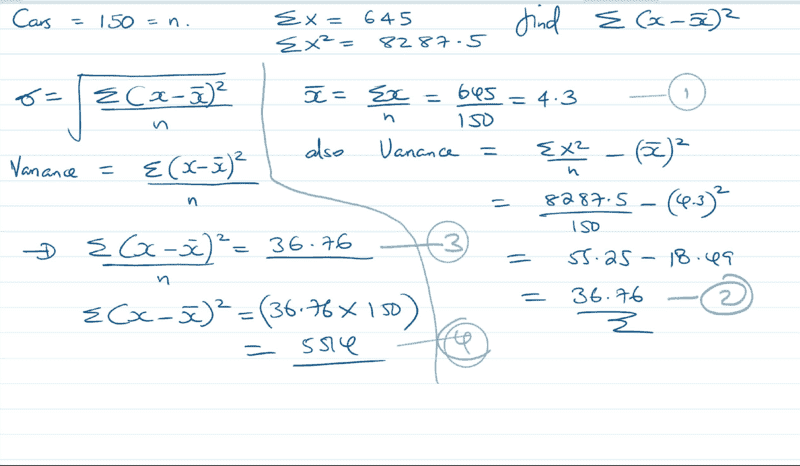 the mark scheme for the question is below here;
the mark scheme for the question is below here;

i am seeking for any other approach that may be there...am now trying to refresh on stats...bingo!
below is my own working;
i am seeking for any other approach that may be there...am now trying to refresh on stats...bingo!