anemone
Gold Member
MHB
POTW Director
- 3,851
- 115
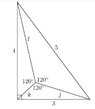
Given positive real values $a,\,b,\,c$ such that
$a^2+b^2+ab=9$
$b^2+c^2+bc=16$
$c^2+a^2+ca=25$
Evaluate $(a+b+c)^2$.
Note:
If you've noticed that I've already posted this problem before, please kindly send me a PM so I could delete this one. Thanks in advance.
$a^2+b^2+ab=9$
$b^2+c^2+bc=16$
$c^2+a^2+ca=25$
Evaluate $(a+b+c)^2$.
Note:
If you've noticed that I've already posted this problem before, please kindly send me a PM so I could delete this one. Thanks in advance.