Solving Alternate Current Homework on R, Impedance, Phase Difference

[fluidistic]

Homework Statement

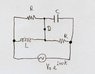
See picture for situation.
1)Demonstrate that if we don't want current flowing at point D, we need R=\sqrt{\frac{L}{C}}.
2)If R satisfies the above condition, find the equivalent impedance of the circuit.
3)Find the angle difference of phase between the current circulating by the emf and by the branch RC. (I find it very confusing as which is the RC branch).

Homework Equations

None given.

The Attempt at a Solution

I'm really weak at alternate current problems.
I know that V(t)=ZI(t). So I must set V(t)=0 in the branch containing D. But I'm having a hard time figuring out V(t) in this branch.
V(t) in the emf branch is V_0 e^{i\omega t}.
I need a little push in the right direction as to reach V(t) in the D-branch. I've thought about Kirchhoff's laws, but in an alternate circuit, I've no idea if I can use them at all.
Thanks.

 

[berkeman]

To get no current in the D branch, there must be no difference in votage between the midpoints of the top and middle branches. That will only be true if the respective voltage divider equations give the same voltage v(f) for the two midpoints.

Does that help, or is that already obvious to you? And where did your avatar go?

 

[fluidistic]

Thanks for the help!

To get no current in the D branch, there must be no difference in votage between the midpoints of the top and middle branches.

This is obvious to me until here.

That will only be true if the respective voltage divider equations give the same voltage v(f) for the two midpoints.

Does that help, or is that already obvious to you?

I don't understand what you mean by "voltage divider equations". Do you mean the potential difference between say the left point on the figure and the upper one?
And also, the potential difference from the right point to the point at the bottom of D?
I don't believe I'm understand it well. Because if it were so, then L wouldn't appear.

And where did your avatar go?

My premium account expired and I have monetary problems and will have them for the next months so I couldn't renew it.

 

[berkeman]

For the voltage divider thing, rotate the diagram 90 degrees clockwise, and call the bottom node ground. The top node is driven by the AC source, and disconnect the short at D. Now write the two voltage divider equations for the two midpoints (call them both Vd(f) ), and set them equal. Use the complex impedances for the inductor and capacitor in the equations.

Are you familiar with the phasor notation for complex impedances? That's all you need to use in this problem, IMO. You don't need to get the complex exponentials involved in the calculations.

EDIT -- or more naturally, Vd(omega)

 

[fluidistic]

For the voltage divider thing, rotate the diagram 90 degrees clockwise, and call the bottom node ground.

Ok!

The top node is driven by the AC source, and disconnect the short at D.

Hmm, I don't really understand what you mean. The top node is the left node of the figure I posted, right?

Now write the two voltage divider equations for the two midpoints (call them both Vd(f) ), and set them equal. Use the complex impedances for the inductor and capacitor in the equations.

I'm sorry, I still don't know what you mean by "voltage divider". Ok for the impedances... but I can't get any equation.

Are you familiar with the phasor notation for complex impedances? That's all you need to use in this problem, IMO. You don't need to get the complex exponentials involved in the calculations.

EDIT -- or more naturally, Vd(omega)

I don't think I'm familiar with this notation. I do know the exponential form of complex numbers however.

 

[berkeman]

For the voltage divider in the DC case...

Say you have two resistors, Rtop and Rbot arranged in series vertically. Vi is at the top and ground is at the bottom. Then the voltage in the middle of that voltage divider is:

V_m = V_i \frac{R_b}{R_t + R_b}

For the AC case with phasors, you just substitute the AC impedance for each component, which depends on the angular frequency omega for inductors and caps.

 

[berkeman]

And just to clarify, the complex impedance of the inductor and capacitor are:

Z_L = j \omega L

Z_C = \frac{1}{j \omega C}

Do those look familiar?

 

[fluidistic]

For the voltage divider in the DC case...

Say you have two resistors, Rtop and Rbot arranged in series vertically. Vi is at the top and ground is at the bottom. Then the voltage in the middle of that voltage divider is:

V_m = V_i \frac{R_b}{R_t + R_b}

For the AC case with phasors, you just substitute the AC impedance for each component, which depends on the angular frequency omega for inductors and caps.

Sounds interesting, I never heard of such a thing as this method. I don't fully grasp it. In my brain, a voltage is a difference of potential between 2 points. If you ask me the voltage in 1 point, I'm tempted to say "0 V". I guess I should look in Internet to learn about this method. I'll try to work my way through it.
Thanks for all... and if I need help I'll ask here.

 

[fluidistic]

And just to clarify, the complex impedance of the inductor and capacitor are:

Z_L = j \omega L

Z_C = \frac{1}{j \omega C}

Do those look familiar?

Yes they look familiar :). I wrote down those on my draft.

 

[berkeman]

Sounds interesting, I never heard of such a thing as this method. I don't fully grasp it. In my brain, a voltage is a difference of potential between 2 points. If you ask me the voltage in 1 point, I'm tempted to say "0 V". I guess I should look in Internet to learn about this method. I'll try to work my way through it.
Thanks for all... and if I need help I'll ask here.

When we speak of "a" voltage, and don't specify a 2nd point for the voltage difference, then ground is implied to be the 2nd point. So the voltage divider equation is ground referenced as I wrote it above. Your original circuit has no explicit ground, so you are free to put it wherever is most convenient for visual appearance and for ease of calculation.

 

[fluidistic]

When we speak of "a" voltage, and don't specify a 2nd point for the voltage difference, then ground is implied to be the 2nd point. So the voltage divider equation is ground referenced as I wrote it above. Your original circuit has no explicit ground, so you are free to put it wherever is most convenient for visual appearance and for ease of calculation.

I don't know how to thank you. I just checked out in wikipedia http://en.wikipedia.org/wiki/Voltage_divider. Wow, amazing I wasn't taught this, nor did I saw it in my books. I've reached R=\sqrt {\frac{L}{C}}!
Now I'll try to solve the rest of the exercise. In any case, as you know, I'm going to ask help here.

 

[fluidistic]

For the impedance of the circuit: am I right if I write Z=\frac{1}{X_L}+\frac{2}{R}+\frac{1}{X_C}=\frac{2}{R}+i\left ( \omega C - \frac{1}{\omega L} \right )? It is considering all circuit components as in parallel.

 

[berkeman]

For the impedance of the circuit: am I right if I write Z=\frac{1}{X_L}+\frac{2}{R}+\frac{1}{X_C}=\frac{2}{R}+i\left ( \omega C - \frac{1}{\omega L} \right )? It is considering all circuit components as in parallel.

All the components are not in parallel. There is a branch that has an R and C in series, and a branch that has an R and an L in series. These two branches are then in parallel. So first write the series impedance for each of the two branches, and then use the parallel combination formula to combine them into a single impedance. Show your work! (and good job, BTW)

 

[fluidistic]

All the components are not in parallel. There is a branch that has an R and C in series, and a branch that has an R and an L in series. These two branches are then in parallel. So first write the series impedance for each of the two branches, and then use the parallel combination formula to combine them into a single impedance. Show your work! (and good job, BTW)

Ok thanks. I don't realize why the RC branch is in series and the LR branch is. All this because of the D branch. For me, the current passing through L has the choice whether to pass by D or R (the right R in the original sketch).
But following your words, Z=\frac{1}{i\omega L+R}+\frac{i\omega C}{R i \omega C +1}, simplifying this is just arithmetics.

 

[berkeman]

Ok thanks. I don't realize why the RC branch is in series and the LR branch is. All this because of the D branch. For me, the current passing through L has the choice whether to pass by D or R (the right R in the original sketch).
But following your words, Z=\frac{1}{i\omega L+R}+\frac{i\omega C}{R i \omega C +1}, simplifying this is just arithmetics.

The premise of the question was that there be no current through the D branch, therefore no difference in voltage. So in calculating the overall Z, you assume no cross-current, and just add the two parallel branches accordingly. Good job.

 

[fluidistic]

The premise of the question was that there be no current through the D branch, therefore no difference in voltage. So in calculating the overall Z, you assume no cross-current, and just add the two parallel branches accordingly. Good job.

Yeah thanks a lot for all. I realized this a few hours after posting if I recall well.