Discussion Overview
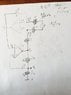
The discussion revolves around solving a circuit problem involving ideal operational amplifiers (op amps). Participants are attempting to determine the voltage difference (v1 - v2) and the current (iA) in a circuit with given resistors and voltage sources, using techniques such as node analysis and superposition. The conversation includes various approaches and assumptions regarding the behavior of the op amps and the circuit configuration.
Discussion Character
- Homework-related
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant attempts to solve the problem using node analysis, assuming no current flows into the op amp outputs, which is later challenged by others.
- Another participant suggests that the assumption of no current flowing into the op amp output is incorrect and advises a reevaluation of the approach.
- Concerns are raised about the voltage expressions used in the initial analysis, prompting requests for more detailed work to identify errors.
- Participants discuss the nature of the input signal, questioning whether it has a ground reference or is floating, which affects the analysis.
- Some participants propose using the superposition theorem to simplify the problem, suggesting it could lead to a straightforward solution.
- There is a suggestion that the op amps should not be replaced by shorts in the circuit analysis, emphasizing the need to treat them correctly in calculations.
- One participant expresses doubt about their ability to solve the problem and seeks assistance, indicating a lack of confidence in their understanding of the material.
- Another participant offers to discuss the problem via Google Hangouts for more effective communication.
- Finally, a participant encourages breaking down the problem into smaller parts, focusing on current flow through the resistors and the outputs of the op amps.
Areas of Agreement / Disagreement
Participants generally agree on the need to reconsider assumptions about current flow in the op amps and the use of superposition, but there is no consensus on the correct approach to solving the problem. Multiple competing views and methods remain in the discussion.
Contextual Notes
There are unresolved assumptions regarding the circuit configuration, the nature of the input signal, and the correct treatment of op amp outputs in the analysis. Participants have not reached a definitive solution or agreement on the methodology.