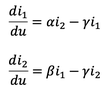Solving coupled equations analytically

[asifadio]

Homework Statement

I'm trying to solve this coupled equation analytically. My strategy is to convert it into the Bernoulli’s form. But as you can see on my attempt, i got stuck on it.

Relevant Equations

I failed to convert it to Bernoulli’s form and now kinda ran out of ideas.

The equation is as attached where,
- α, β and γ are constants
- i1 and i2 are the variables.

Also attached, is my attempt and where I stuck at.

If anyone has an idea how to convert this into Bernoulli’s form, please I really need help. If there are any other ideas please let me know too..

Really appreciate it in advance!

Thank you.
Asif

 

[Delta2]

Solve the second for $i_1$ and from this expression that you find for $i_1$ calculate also $\frac{di_1}{du}$ which will be an expression containing $\frac{d^2i_2}{du^2}$ and $\frac{di_2}{du}$.

Then go back in the first and replace $i_1$ with what you found and also replace $\frac{di_1}{du}$ with what you found.

If all go well, I think you ll find a second order linear ODE for $i_2$.

 

[epenguin]

You can do it the way just suggested.
But then how do you solve the second order differential equation? Usually you try the solution i₁= e^λu and you find that leads to a quadratic in λ.
However you can equally well try the same solution in the original pair of equations and it will lead you to the same result.

Good that you tried to work out a way yourself. The time will not have been wasted. It will have helped you when you go as you now should to your textbook and where you will find this is absolutely all very standard stuff.
In fact it has often seemed to me that everything students have done up to where you are now in math, linear algebraic equations, polynomials, trigonometry, complex numbers,… has had the purpose of leading them to linear differential equations where that and also physics stuff all come together.

Important to realize that n first order differential equations in n variables are equivalent to or can be changed into one $n$-th order one In one variable, and vice versa. And pretty much the same thing for second order or other orders.