Wavefunction
- 99
- 4
Homework Statement
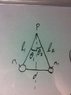
Two masses m_1 and m_2 (m_1 ≠ m_2) are connected by a rigid rod of length d and of negligible
mass. An extensionless string of lengthl_1 is attached to m_1 and connected to a fixed point P.
Similarly, a string of length l_2 (l_1 ≠ l_2) connects m_2 and P. Obtain the equation describing the
motion in the plane of m_1, m_2, and P and find the frequency of small oscillations around the
equilibrium position.
Homework Equations
(1) \frac{∂L}{∂q_j}-\frac{d}{dt}\frac{∂L}{∂\dot{q_j}}+\sum_kλ_k(t)\frac{∂f_k(q_j,t)}{∂q_j} = 0
(2) s=Dn-m
The Attempt at a Solution
Okay so the first thing I did in this problem was I tried to figure out how many coordinates I need. Each particle can move in 2 dimensions so D=2. There are 2 particles so n=2. There are 3 constraints:(a) x_1^2+y_1^2 = l_1^2, (b) x_2^2+y_2^2 = l_1^2, and (c) (x_2-x_1)^2+(y_2-y_1)^2 = d^2
s=(2*2)-3 = 1 However, I'll start of with the original four coordinates and work my way to only 1:
The Lagrangian:
L=T-U → T=\frac{m_1}{2}[\dot{x_1}^2+\dot{y_1}^2]+\frac{m_2}{2}[\dot{x_2}^2+\dot{y_2}^2] and U=g[m_1y_1+m_2y_2]
Then L=\frac{m_1}{2}[\dot{x_1}^2+\dot{y_1}^2]+\frac{m_2}{2}[\dot{x_2}^2+\dot{y_2}^2]-g[m_1y_1+m_2y_2]
Now I can apply 2 out of my 3 constraints (a and b):
x_1 = l_1sin(θ_1)
y_1 = l_1cos(θ_1)
x_2 = l_2sin(θ_2)
y_2 = l_2cos(θ_2)
Applying these transformations to the Lagrangian:
L=\frac{1}{2}[m_1l_1^2\dot{θ_1}^2+m_2l_2^2\dot{θ_2}^2]-g[m_1l_1cos(θ_1)+m_2l_2cos(θ_2)]
Now the angular velocity \dot{θ} is the same for both particles because the thin massless rod of length d holds them together. So \dot{θ_1}=\dot{θ_2}
Applying this to L:
L=\frac{1}{2}[m_1l_1^2+m_2l_2^2]\dot{θ_1}^2-g[m_1l_1cos(θ_1)+m_2l_2cos(θ_2)]
In addition:
\dot{θ_1}=\dot{θ_2} → θ_1=θ_2+C → f = θ_1-θ_2-C=0
Okay now I can use eq. (1):
θ_1: \frac{∂L}{∂θ_1} = g[m_1l_1sin(θ_1)], \frac{d}{dt}[\frac{∂L}{∂\dot{θ_1}}] = \frac{d}{dt}[[m_1l_1^2+m_2l_2^2]\dot{θ_1}], and λ\frac{∂f}{∂θ_1} = λ
(3) g[m_1l_1sin(θ_1)]-[m_1l_1^2+m_2l_2^2]\ddot{θ_1}+λ=0
θ_2: \frac{∂L}{∂θ_2} = g[m_2l_2sin(θ_2)], \frac{d}{dt}[\frac{∂L}{∂\dot{θ_2}}] = \frac{d}{dt}[0], and λ\frac{∂f}{∂θ_1} = -λ
(4) g[m_2l_2sin(θ_2)]-λ=0
From eq. 4 I know λ in terms of θ_1:
Using θ_1-C=θ_2; λ=g[m_2l_2sin(θ_1-C)]
Then eq. 3 becomes:
g[m_1l_1sin(θ_1)]-[m_1l_1^2+m_2l_2^2]\ddot{θ_1}+g[m_2l_2sin(θ_1-C)]=0
g[m_1l_1sin(θ_1)]+g[m_2l_2[sin(θ_1)cos(C)-sin(C)cos(θ_1)]]-[m_1l_1^2+m_2l_2^2]\ddot{θ_1}=0<br />
[gm_1l_1+gm_2l_2cos(C)]sin(θ_1)-gm_2l_2sin(C)cos(θ_1)-[m_1l_1^2+m_2l_2^2]\ddot{θ_1}=0<br />
Now there is the matter of C to handle:
If I plug in the coordinate transforms into constraint (c) I will arrive at the law of cosines:
l_1^2+l_2^2-2l_1l_2cos(θ_1-θ_2) = d^2 (keep in mind here that I have defined θ_1 < 0 and θ_2>0)
From the law of cosines I get:
θ_1 = θ_2+arccos(\frac{d^2-l_1^2-l_2^2}{-2l_1l_2}) so I have now found what C is:
C = arccos(\frac{d^2-l_1^2-l_2^2}{-2l_1l_2})
Now plugging in C into the new form of eq. 3:
[gm_1l_1+gm_2l_2cos(arccos(\frac{d^2-l_1^2-l_2^2}{-2l_1l_2}))]sin(θ_1)-gm_2l_2sin(arccos(\frac{d^2-l_1^2-l_2^2}{-2l_1l_2}))cos(θ_1)-[m_1l_1^2+m_2l_2^2]\ddot{θ_1}=0<br />
[gm_1l_1+gm_2l_2(\frac{d^2-l_1^2-l_2^2}{-2l_1l_2})]sin(θ_1)-gm_2l_2(\frac{\sqrt{(-2l_1l_2)^2-(d^2-l_1^2-l_2^2)^2}}{-2l_1l_2})cos(θ_1)-[m_1l_1^2+m_2l_2^2]\ddot{θ_1}=0<br />
Okay so now I only want to consider small oscillations about the equilibrium position \Rightarrow θ_1\ll 1
Then eq. 3 becomes the Linear ODE:
g[m_1l_1-m_2(\frac{d^2-l_1^2-l_2^2}{2l_1})](θ_1)+gm_2(\frac{\sqrt{(-2l_1l_2)^2-(d^2-l_1^2-l_2^2)^2}}{2l_1})(1)-[m_1l_1^2+m_2l_2^2]\ddot{θ_1}=0<br />
Now this equation can be put into the form \ddot{θ}+ω_0^2θ=f(t) where f(t) is a constant driving force.
\ddot{θ_1}+\frac{-g[m_1l_1-m_2(\frac{d^2-l_1^2-l_2^2}{2l_1})]}{m_1l_1^2+m_2l_2^2}θ_1=\frac{gm_2(\frac{\sqrt{(-2l_1l_2)^2-(d^2-l_1^2-l_2^2)^2}}{2l_1})}{m_1l_1^2+m_2l_2^2}<br />
Now then ω_0^2 \equiv \frac{-g[m_1l_1-m_2(\frac{d^2-l_1^2-l_2^2}{2l_1})]}{m_1l_1^2+m_2l_2^2} (frequency of oscillation about the equilibrium point)
The equilibrium condition is given as θ_1(0) = \frac{f(t)}{ω_0^2} because in equilibrium \ddot{θ_1(t=0)}=0 In this case f(t) = \frac{gm_2(\frac{\sqrt{(-2l_1l_2)^2-(d^2-l_1^2-l_2^2)^2}}{2l_1})}{m_1l_1^2+m_2l_2^2}<br />
The general solution to eq 3. is:
(4) θ_1(t) = Acos(ω_0t)+Bsin(ω_0t)+θ_p(t)
\ddot{θ_p}+ω_0^2θ_p = gm_2(\frac{\sqrt{(-2l_1l_2)^2-(d^2-l_1^2-l_2^2)^2}}{2l_1}) → θ_p = gm_2(\frac{\sqrt{(-2l_1l_2)^2-(d^2-l_1^2-l_2^2)^2}}{2ω_0^2l_1})
A = θ_1(0)-θ_p then eq. 4 becomes θ_1(t) = [θ_1(0)-θ_p]cos(ω_0)+Bsin(ω_0t)+θ_p
\dot{θ_1} = Bω_0cos(ω_0t) → \dot{θ_1(0)} = Bω_0 → B=\frac{ \dot{θ_1(0)}}{ω_0}
So the general solution is then:
θ_1(t) = [θ_1(0)-θ_p]cos(ω_0t)+\frac{ \dot{θ_1(0)}}{ω_0}sin(ω_0t)+θ_p
Thank you in advance for helping me out in checking my work(: