Find the equation of motion using the Lagrangian for this Atwood machine

[Istiak]

Homework Statement

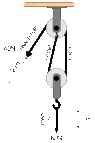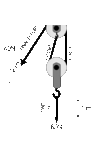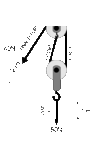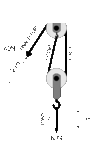
Find equation of motion using Lagrangian of Atwood machine

Relevant Equations

L=T-U
$\frac{d}{dt}(\frac{\partial L}{\partial \dot{q}})=\frac{\partial L}{\partial q}$

My understanding of the system from the image (which was given in book)

I could see there's 3 tension in 2 body. Even I had seen 2 tension in a body. It was little bit confusing to me. I could find tension in Lagrangian from right side. But left side was confusing to me.

$$L=\frac{1}{2}m_1\dot{x}^2+\frac{1}{2}m_2\dot{x}^2$-m_1gx-m_2g(l-x)-m_2g(l_1-x)$$
Here $l-x$ is representing the potential energy for "center rope" tension and l_1-x is representing tension for right one.

After using Euler form and rearranging I get that

$$\ddot{x}=\frac{2m_2-m_1}{m_1+m_2}g$$

I don't know if the answer is correct. I know that the acceleration is for whole body. But in the book, they had found separated acceleration

From their equation it's like actually my answer is wrong.

 

[BvU]

Hi,

Your expose is rather confusing to me. You don't say what $x$ is. $l$ ? $l_1$ ?

Are you suggesting $m_1$ and $m_2$ both move with velocity $\dot x$ ?

$\$

 

[Istiak]

Yes! I am assuming that both object moves at same speed which I denoted by $dot x$. And l and l_1 is constant length. l is from left to center (where object m_2 is connected. And l_1 is right side length. I was thinking there's two tension hence they will act different way hence had taken separated length.

When first object is moving then it will pull the rope either (earlier i was thinking that the object is attached with the rope but its not hence my assumption was wrong.)

My mind was stucked with two tension and two body. But the system was messy by additional tension which i was unable to understand hence i am thinking that my idea behind $x$ was also wrong.

 

[BvU]

Why not make two drawings, with m1 in two different postions, and measure !

$\$

 

[Haorong Wu]

Why are you assuming $m_1$ and $m_2$ share the same velocity?

 

[wrobel]

Direct an axis $z$ downwards vertically and let $z_1,z_2$ be coordinates of the particles. Find a relation between $z_1,z_2$. Use the length of the string. Differentiate the relation in time

 

[Istiak]

I was trying to do the solution another way. What still disturbing me that is third no. tension. I was thinking if I should consider another kinetic energy in terms of third tension. In my new step, I was assuming that there's another K.E. in terms third tension.

$$L=\frac{1}{2}m_1\dot{x}^2+\frac{1}{2}m_2\dot{x}^2+\frac{1}{2}m_2\dot{x}^2-m_2gx-m_2g(l_b-l_a-x)-m_2g(l_a-x)$$
After using Euler-Lagrange,
$$\ddot{x}=\frac{2m_2-m_1}{m_1+2m_2}g$$

Is my answer correct now? I think it's not correct cause, there won't be 3 K.E for only 2 body. There must be 2 K.E. for 2 body we just have to rearrange them. So I think the accurate answer is
$$\ddot{x}=\frac{2m_2-m_1}{m_1+m_2}g$$

 

[Lnewqban]

1) There is no way for the tension of the rope to magically change between the point of anchorage to the ceiling and the opposite end.

2) During the same time, body of mass m2 moves distance d and body of mass m1 moves 2d; therefore, bodies 1 and 2 can't have same average velocities or instantaneous accelerations.

3) The function of the fixed-to-ceiling pulley is only to change the direction of the rope and its associate tension, but the function of the moving pulley is more complicated: it is also a simple machine providing a mechanical advantage of value 2.

4) Note the values to which a1 and a2 tend to when the values of m2 and m1 tend to zero in the solution equations shown in the book. What rate of m1/m2 would stop the system from acelerating in any direction?

Please, see:
http://hyperphysics.phy-astr.gsu.edu/hbase/atwd.html#c3