Filip Larsen said:
Given that ##A, B, X \in \text{SO(3)}## and given that ##A, B \neq I## and ##A \neq B##, then find any ##X## such that
$$A X = X B .$$
Since this equation represent 9 equations in the 9 unknown elements of ##X## and there are 9 more equations from orthogonality of SO(3), i.e. ##X X^T = I## intuition tells me it should be solvable, but my intuition also tries to tell me that surely there must exist a methods for such equations that does not involve explicitely solving for 9 uknowns in 18 equations. However, so far none of the symbolic or numeric methods in my engineering toolbox seems to come close. So, what tool am I missing in my toolbox for this?
@Filip Larsen After all this time, are you still interested in solving your equation? Because by using 3D vector geometry, you can find all the solutions for your matrix ##X## simply by inspection!
While it's true that an arbitrary ##\text{SO(3)}## rotation matrix ##R##, where ##RR^{T}=I##, contains 9 entries, those entries all depend ultimately on only 3 parameters: a unit-vector ##\boldsymbol{\hat{n}}_{R}\equiv\cos\phi\sin\theta\boldsymbol{\hat{x}}+\sin\phi\sin\theta\boldsymbol{\hat{y}}+\cos\theta\boldsymbol{\hat{z}}## that defines the axis-of-rotation (2 parameters) and a rotation-angle ##\rho## about that axis (1 parameter). This "angle-axis" parameterization of ##R=R\left(\boldsymbol{\hat{n}}_{R};\rho\right)## is expressed in component-form as (
https://scipp.ucsc.edu/~haber/ph216/rotation_12.pdf eq.(19)):$$R^{i}{}_{j}\equiv\cos\rho\,\delta^{i}{}_{j}+\left(1-\cos\rho\right)\hat{n}_{R}^{i}\hat{n}_{Rj}-\sin\rho\,\epsilon^{i}{}_{jk}\hat{n}_{R}^{k}\tag{1}$$and has trace:$$\text{tr}R\equiv\delta^{j}{}_{i}R^{i}{}_{j}=2\cos\rho+1\tag{2}$$That is, ##\text{tr}R## depends only on the rotation angle ##\rho##. This is important because your equation ##AX=XB## necessarily imposes one constraint between the otherwise arbitrary pair of matrices ##A,B##, as can be seen by rewriting it in the form ##A=XBX^{T}\Rightarrow\mathrm{tr}A=\mathrm{tr}\left(XBX^{T}\right)=\mathrm{tr}\left(X^{T}XB\right)=\mathrm{tr}B##. Per (2), this means that the rotation angles ##\alpha,\beta## characterizing ##A,B## must be the same (up to a sign, which can always be absorbed by flipping the direction of one of the rotation axes ##\boldsymbol{\hat{n}}_{A}## or ##\boldsymbol{\hat{n}}_{B}##). In other words, your equation mandates that the general forms of ##A,B## must be:$$A=R\left(\boldsymbol{\hat{n}}_{A};\alpha\right),\;B=R\left(\boldsymbol{\hat{n}}_{B};\alpha\right)\tag{3a,b}$$To now solve your equation for ##X##, note that ##XBX^{T}=A## can be interpreted as saying that the matrix transformation you seek rotates the rank-2 tensor ##B## into the tensor ##A##. In turn, by (3) this means that ##X## rotates the rank-1 vector ##\boldsymbol{\hat{n}}_{B}## into the vector ##\boldsymbol{\hat{n}}_{A}##; i.e., ##X\boldsymbol{\hat{n}}_{B}=\boldsymbol{\hat{n}}_{A}##. So you're looking for matrices ##X## that simply rotate one unit-vector into another. Denoting by ##\mathcal{P}## the plane spanned by the vectors ##\boldsymbol{\hat{n}}_{A}## and ##\boldsymbol{\hat{n}}_{B}##, the 2 possible solution-forms for ##X## can be "read-off" from the following diagram:
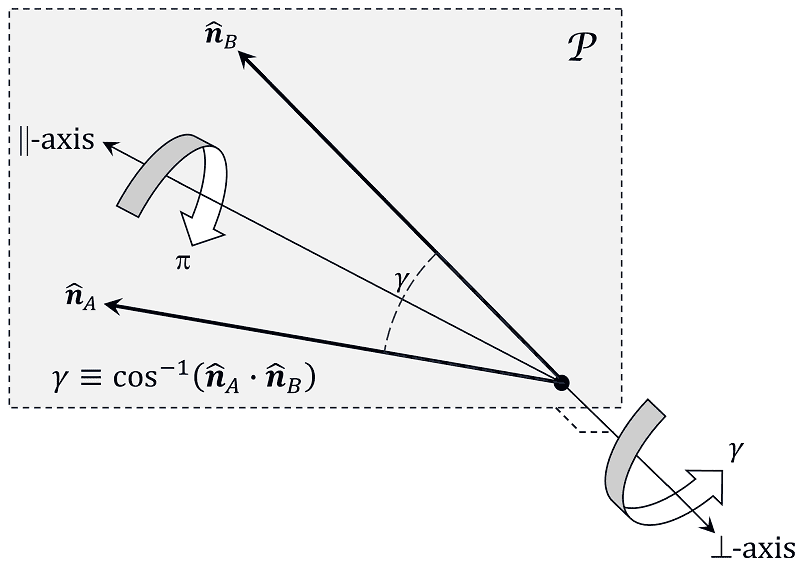
First, consider a rotation-axis ("##\parallel\mathrm{axis}##") in the plane ##\mathcal{P}##, that bisects the angle ##\cos^{-1}\left(\boldsymbol{\hat{n}}_{A}\cdotp\boldsymbol{\hat{n}}_{B}\right)## between ##\boldsymbol{\hat{n}}_{A}## and ##\boldsymbol{\hat{n}}_{B}## (i.e., the axis points in the direction of ##\boldsymbol{\hat{n}}_{A}+\boldsymbol{\hat{n}}_{B}##). Rotating ##\boldsymbol{\hat{n}}_{B}## about that axis through an angle of ##\pi## radians sweeps ##\boldsymbol{\hat{n}}_{B}## out of the plane through a half-cone into coincidence with ##\boldsymbol{\hat{n}}_{A}##. Call this solution ##X^{\parallel}##. Alternatively, choose a rotation-axis ("##\perp\mathrm{axis}##") normal to plane ##\mathcal{P}## (i.e., the axis points in the direction of ##\boldsymbol{\hat{n}}_{B}\times\boldsymbol{\hat{n}}_{A}##) and rotate ##\boldsymbol{\hat{n}}_{B}## in the plane by the angle ##\cos^{-1}\left(\boldsymbol{\hat{n}}_{A}\cdotp\boldsymbol{\hat{n}}_{B}\right)## to align ##\boldsymbol{\hat{n}}_{B}## with ##\boldsymbol{\hat{n}}_{A}##. This gives the second solution ##X^{\perp}##. Explicitly:$$X^{\parallel}=R\left(\frac{\boldsymbol{\hat{n}}_{A}+\boldsymbol{\hat{n}}_{B}}{\left\Vert \boldsymbol{\hat{n}}_{A}+\boldsymbol{\hat{n}}_{B}\right\Vert };\pi\right),\;X^{\perp}=R\left(\frac{\boldsymbol{\hat{n}}_{B}\times\boldsymbol{\hat{n}}_{A}}{\left\Vert \boldsymbol{\hat{n}}_{B}\times\boldsymbol{\hat{n}}_{A}\right\Vert };\cos^{-1}\left(\boldsymbol{\hat{n}}_{A}\cdotp\boldsymbol{\hat{n}}_{B}\right)\right)\tag{4a,b}$$ So these 2 rotation matrices (as well as their negatives) satisfy ##0=AX^{\parallel,\perp}-X^{\parallel,\perp}B## as desired.
But masochist that I am, I want to verify this using actual matrix algebra. I'll spare you the display here of the general form of ##R\left(\boldsymbol{\hat{n}}_{R};\rho\right)## with its 9 entries, but you can find it as eq.(20) in the reference cited above. Instead, without loss of generality, I make a judicious choice of cartesian coordinates to simplify the explicit forms of the matrices ##A,B,X^{\parallel},X^{\perp}##. First, I take the ##z##-axis to align with the rotation-axis ##\boldsymbol{\hat{n}}_{A}##:$$
A\equiv R\left(\boldsymbol{\hat{z}};\alpha\right)=\begin{pmatrix}\cos\alpha & -\sin\alpha & 0\\
\sin\alpha & \cos\alpha & 0\\
0 & 0 & 1
\end{pmatrix}
\tag{5}$$Then I choose the ##x,y## axes so that the rotation-axis ##\boldsymbol{\hat{n}}_{B}## lies entirely in the ##xz## plane; i.e., ##\boldsymbol{\hat{n}}_{B}=\pm\sin\theta\boldsymbol{\hat{x}}+\cos\theta\boldsymbol{\hat{z}}##:$$B_{\pm}\equiv R\left(\pm\sin\theta\boldsymbol{\hat{x}}+\cos\theta\boldsymbol{\hat{z}};\alpha\right)$$$$
=\begin{pmatrix}\cos\alpha\cos^{2}\theta+\sin^{2}\theta & -\sin\alpha\cos\theta & \pm\left(1-\cos\alpha\right)\cos\theta\sin\theta\\
\sin\alpha\cos\theta & \cos\alpha & \mp\sin\alpha\sin\theta\\
\pm\left(1-\cos\alpha\right)\cos\theta\sin\theta & \pm\sin\alpha\sin\theta & \cos\alpha\sin^{2}\theta+\cos^{2}\theta
\end{pmatrix}
\tag{6}$$With these choices, eq.(4) becomes:$$
X_{\pm}^{\parallel}\equiv R\left(\pm\sin\frac{\theta}{2}\boldsymbol{\hat{x}}+\cos\frac{\theta}{2}\boldsymbol{\hat{z}};\pi\right)=\begin{pmatrix}-\cos\theta & 0 & \pm\sin\theta\\
0 & -1 & 0\\
\pm\sin\theta & 0 & \cos\theta
\end{pmatrix}
\tag{7a}$$$$
X_{\pm}^{\perp}=R\left(\mp\boldsymbol{\hat{y}};\theta\right)=\begin{pmatrix}\cos\theta & 0 & \mp\sin\theta\\
0 & 1 & 0\\
\pm\sin\theta & 0 & \cos\theta
\end{pmatrix}
\tag{7b}$$Finally, throwing matrices (5), (6) and (7) into Mathematica confirms that:$$0=AX_{\pm}^{\parallel,\perp}-X_{\pm}^{\parallel,\perp}B_{\pm}\tag{8}$$is indeed true.
(Whew, I'm exhausted!)