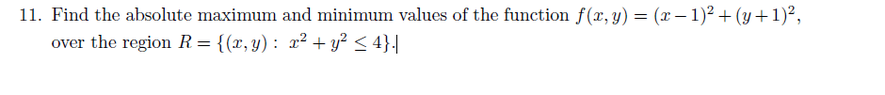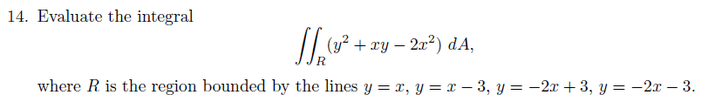Vanrichten
- 12
- 1
Ok the first problem is The output Q of an economic system subject to two inputs, such as labor L and capital K, soften modeled by the Cobb-Douglas production function Q(L;K) = cLaKb, where a; b and c
are positive real numbers. When a+b = 1, the case is called constant returns to scale. Suppose
a = 1
3 , b = 2
3 and c = 40.
A) If L is held constant at L = 10, write the function that gives the dependence of Q on K.
B) If K is held constant at K = 15, write the function that gives the dependence of Q on L
Does this look ok Name: View attachment 1681
Next I have this problem View attachment 1682
I'm pretty sure you have to use Lagrange multipliers on this one I know you first need to take partial derivatives of the function then set up the scalar equations involving lamba, I know that much but I'm stuck there.
The third problem I have is this View attachment 1683For this problem I graphed it out and you can see that there are two sets of parallel lines and the region is rectangular so I think you can use a change of variable. I tried v=y and u=2x+y but it didn't work
are positive real numbers. When a+b = 1, the case is called constant returns to scale. Suppose
a = 1
3 , b = 2
3 and c = 40.
A) If L is held constant at L = 10, write the function that gives the dependence of Q on K.
B) If K is held constant at K = 15, write the function that gives the dependence of Q on L
Does this look ok Name: View attachment 1681
Next I have this problem View attachment 1682
I'm pretty sure you have to use Lagrange multipliers on this one I know you first need to take partial derivatives of the function then set up the scalar equations involving lamba, I know that much but I'm stuck there.
The third problem I have is this View attachment 1683For this problem I graphed it out and you can see that there are two sets of parallel lines and the region is rectangular so I think you can use a change of variable. I tried v=y and u=2x+y but it didn't work