Joran Verlaeck
- 2
- 0
Dear Forum Users,
I am studying physics on my own, i am new to this forum, i am working every example in the book and i have a question. I hope that you are so kind to give me an explanation so that i can continue my chapter exercises.
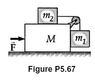
The question of the book is : What horizontal force must be applied to a large block of mass M shown in Figure P5.67 so that the tan blocks remain stationary relative to M ? Assume all surfaces and the pulley are frictionless. (Notice that the force exerted by the string accelerates M1)
See attachement for picture.
The calculation goes as follows.
M1*g - T = 0 =>
T = M2 * a =>
M1*g = M2 * a => a = (M1*g)/(M2)
F = TotalMass * a => in the book and on the internet the result is
F = (M + M1 + M2) * (M1*g) / (M2)
What i was wondering is if M1 is not connected by the string with M2, and the surface is frictionless, normally only block M would slide together with M1 and M2 would remain stationary and eventually fall off. The tension in the robe is provided by the gravitational force, no gravity
no tension. So in the end result F only needs to accelerate M and M1 and not M2 because that
is accelerated by gravity -> equation a = M1 * G / M2.
So why is the result (M + M1 + M2) * (M1*g) / (M2) and not (M + M1) * (M1*g) / (M2).
Because F is not responsible to give M2 that acceleration just for keeping M relative to M2 in rest.
So they both need the same acceleration.
Can you please help me with this reasoning.
Thx
Jöran
I am studying physics on my own, i am new to this forum, i am working every example in the book and i have a question. I hope that you are so kind to give me an explanation so that i can continue my chapter exercises.
The question of the book is : What horizontal force must be applied to a large block of mass M shown in Figure P5.67 so that the tan blocks remain stationary relative to M ? Assume all surfaces and the pulley are frictionless. (Notice that the force exerted by the string accelerates M1)
See attachement for picture.
The calculation goes as follows.
M1*g - T = 0 =>
T = M2 * a =>
M1*g = M2 * a => a = (M1*g)/(M2)
F = TotalMass * a => in the book and on the internet the result is
F = (M + M1 + M2) * (M1*g) / (M2)
What i was wondering is if M1 is not connected by the string with M2, and the surface is frictionless, normally only block M would slide together with M1 and M2 would remain stationary and eventually fall off. The tension in the robe is provided by the gravitational force, no gravity
no tension. So in the end result F only needs to accelerate M and M1 and not M2 because that
is accelerated by gravity -> equation a = M1 * G / M2.
So why is the result (M + M1 + M2) * (M1*g) / (M2) and not (M + M1) * (M1*g) / (M2).
Because F is not responsible to give M2 that acceleration just for keeping M relative to M2 in rest.
So they both need the same acceleration.
Can you please help me with this reasoning.
Thx
Jöran