Solving Rotation Physics: Find Net Force for Ball Rolling Down Ramp

[Little Dump]

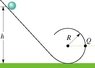
Ok there's this ball rolling down a ramp. The ball has some radius r and some mass m. At the bottom of the ramp there is a loop. The loop has radius R.

The question is, if the ball is 1/4 of the way completed the loop, what is the horizontal component of the net force on the ball. And it is also given that the ball starts up the ramp at height 6R.

Ok so I've been messing around, and what getting me is that when the ball starts the go up in the loop, gravity will do some work. The problem is, I do not know how to calculate the work done by gravity.

Perhaps I am doing the question wrong because I am analysing the rotation of the ball in the loop, not the actual rotation of the ball itself.

Basically what I am doing is using energy and here's my equations

mg(6R) + Wgrav = 1/2mv^2 + 1/2I(omega)^2 + mgR
and
v = R(omega)

so we make the substitution and solve for omega

then we go back and solve for v

the we do

a = v^2/R

and finally

F=ma

but I may be doing this completely wrong so any help will be great. Here is the original question with diagram:




A small solid marble of mass 12 g and radius 3.8 cm will roll without slipping along the loop-the-loop track shown in Fig. 12-33 if it is released from rest somewhere on the straight section of track. (a) From what initial height h above the bottom of the track must the marble be released if it is to be on the verge of leaving the track at the top of the loop? (The radius of the loop-the-loop is 4.0 m; Note that it is much greater than the radius of the marble.) (b) If the marble is released from height 6R above the bottom of the track, what is the horizontal component of the force acting on it at point Q?


The answer with these number is 0.840N.

 

[nautica]

try the "homework" section.

Nautica

 

[M98Ranger]

First of all, I would like to commend you for attempting to solve this problem using energy and rotational motion equations. It shows that you have a good understanding of the concepts involved. However, I believe there are a few mistakes in your approach and equations.

To start off, let's define some variables:
- h: initial height of the ball above the bottom of the track
- R: radius of the loop
- r: radius of the ball
- m: mass of the ball
- g: acceleration due to gravity
- v: velocity of the ball at the top of the loop
- ω: angular velocity of the ball at the top of the loop
- F: net force acting on the ball at point Q

Now, let's analyze the situation using the concepts of energy and rotational motion. At the bottom of the ramp, the ball has some potential energy (mgh) and no kinetic energy (since it is at rest). As it rolls down the ramp, it gains kinetic energy and loses potential energy. At the top of the loop, the ball has some kinetic energy (1/2mv^2) and some rotational kinetic energy (1/2Iω^2), where I is the moment of inertia of a solid sphere (2/5mr^2). The ball also experiences a normal force (N) and a gravitational force (mg). Since the ball is on the verge of leaving the track at the top of the loop, the normal force is equal to zero. This means that the net force acting on the ball is equal to the gravitational force (mg).

Using the conservation of energy, we can equate the initial potential energy to the final kinetic and rotational kinetic energy:
mgh = 1/2mv^2 + 1/2Iω^2
Substituting the value of I and ω (ω = v/r) and solving for v, we get:
v = √(5gh/2)

Now, at the top of the loop, the ball experiences a centripetal force (F = mv^2/R) due to its circular motion. This force is provided by the normal force, which is zero at this point. Therefore, the net force acting on the ball at point Q is equal to the centripetal force:
F = mv^2/R = m(5gh/2)/R = 5mgR/2

Finally, to find