Solving Sub-Problem for OpenAI Lunar Lander v2: Seeking Advice

In summary, the conversation discusses a pet project related to the OpenAI Lunar Lander v2 and the need for help with a sub-problem. The problem involves finding the magnitude of main and side engine thrust, tilted angle of the main engine nozzle, and other variables given certain inputs. The equations seem complex and the speaker is seeking advice on how to solve them, preferably numerically. An analytical solution would be appreciated but is not necessary.
  • #1
genxium
141
2
I'm currently working on a pet project which is similar to the OpenAI Lunar Lander v2 (hence the problem is in a 2D context), and seeking help for a sub-problem that's been blocking me for a while.

At any instant of time, I'm to find
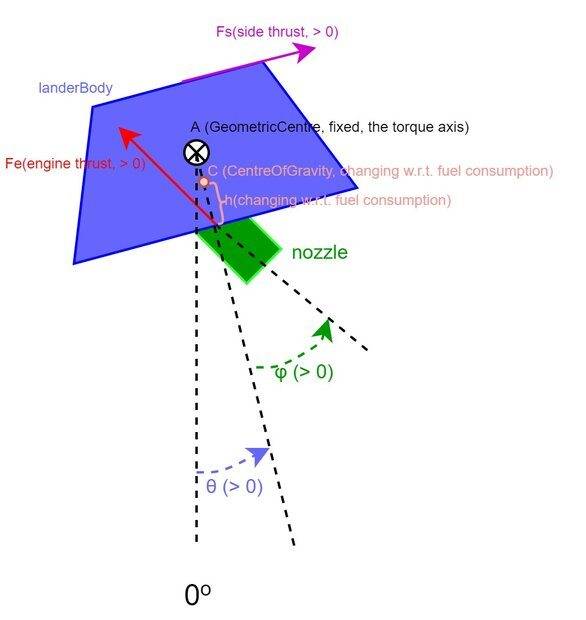
  • Fe: magnitude of main engine thrust, must be >0
  • Fs: magnitude of side engine thrust (>0 to point to the "right w.r.t. lander body", and < 0 to point to opposite direction),
  • φ: tilted angle of main engine nozzle w.r.t. lander body, should be within [-π/2, +π/2]

, given
  • ax: the expected x-acceleration of COG (center of gravity, same below)
  • ay: the expected y-acceleration of COG
  • βC: the expected angular acceleration w.r.t axis through COG and perpendicular to the plane (this screen)
  • m: current mass of the whole lander
  • IC: current moment of inertia of the whole lander w.r.t. same axis of βC
  • θ: current tilted angle of the lander body w.r.t. the fixed gravity direction
  • h: current distance of COG and the nozzle hinge as shown in the figure below
  • g: fixed gravity acceleration
  • H: total height of the lander body
lunarlander_rotation-lunarlander_forces.jpg


To my understanding, the dynamics are (don't know whether I can use TeX here, tried wrapping with $$ and ## but preview didn't work)
  • -Fe*sin(θ+φ) + Fs*cosθ = ax*m
  • Fe*cos(θ+φ) + Fs*sinθ - g*m = ay*m
  • Fe*sinφ*h + Fs*(H-h) = βC*IC
and the "to find variables (in red)" seem non-trivial to solve for.

Is there any advice for solving them at least numerically? An analytical solution will certainly be much appreciated but not a pursuit here.
 
Last edited:
Physics news on Phys.org
  • #2
At a glance it appears your equations can be simplified a bit by expressing the force and torque equations using body coordinates in which input acceleration and gravity are rotated by ##\theta##.
 

FAQ: Solving Sub-Problem for OpenAI Lunar Lander v2: Seeking Advice

How can I improve my performance in solving the sub-problem for OpenAI Lunar Lander v2?

There are a few strategies you can try to improve your performance in solving the sub-problem for OpenAI Lunar Lander v2. First, make sure you have a good understanding of the problem and the environment. This will help you design better algorithms and approaches. You can also try adjusting the hyperparameters of your algorithm, such as the learning rate or exploration rate, to see if that improves your results. Additionally, you can try using more advanced techniques such as reinforcement learning or deep learning to solve the problem.

What are some common challenges when solving the sub-problem for OpenAI Lunar Lander v2?

Some common challenges when solving the sub-problem for OpenAI Lunar Lander v2 include dealing with noisy or incomplete data, choosing appropriate algorithms and parameters, and dealing with a high-dimensional and continuous action space. Additionally, the problem can be quite complex and require a lot of computational power and time to solve. It may also be difficult to find a good balance between exploration and exploitation in the learning process.

Are there any specific tools or libraries that can help with solving the sub-problem for OpenAI Lunar Lander v2?

Yes, there are several tools and libraries that can aid in solving the sub-problem for OpenAI Lunar Lander v2. Some popular options include OpenAI Gym, a toolkit for developing and comparing reinforcement learning algorithms, and TensorFlow, a library for building and training deep learning models. Other useful tools include PyTorch, Keras, and scikit-learn.

How can I evaluate the performance of my solution for the sub-problem of OpenAI Lunar Lander v2?

There are a few ways to evaluate the performance of your solution for the sub-problem of OpenAI Lunar Lander v2. One approach is to use a reward function to measure how well your solution is able to complete the task and achieve the desired goal. You can also compare your results to those of other solutions or benchmarks to see how well you are performing. Additionally, you can use various visualization techniques to analyze and interpret your results.

Are there any ethical considerations to keep in mind when solving the sub-problem for OpenAI Lunar Lander v2?

Yes, there are a few ethical considerations to keep in mind when solving the sub-problem for OpenAI Lunar Lander v2. First, it is important to ensure that your solution is not causing harm or damage to the environment or any individuals. Additionally, you should be transparent about the purpose and potential consequences of your research. It is also important to consider the potential biases and limitations of your solution and work towards creating fair and unbiased algorithms.

Hot Threads

Recent Insights

Back
Top