luidgi93
- 2
- 0
- TL;DR Summary
- A question regarding the boundary conditions for the 1D Poisson equation of a MOS devics (Al - SiO2-Si)
Hey everyone,
I'm currently working on a 1D Poisson Solver for a MOS device (Al-Si-SiO2). Therefore, I programmed a Poisson Solver which is appling a boxintegration (Finite Volume Method) through the structure from φ(0) at the metal-oxide interface and φ(x_bulk = 20 nm) in in the silicon bulk. It is solving the equation system numerically with a Newton Solver. The solver is working properly. ρ is calculated through:
ρ = q0 * (Nd - Na - n + p)
with
n = ni * exp(- φ / (kb [eV] * T)) and p = ni * exp( φ/ (kb [eV] * T))
The current solution is for φ (top) and ρ (bottom):
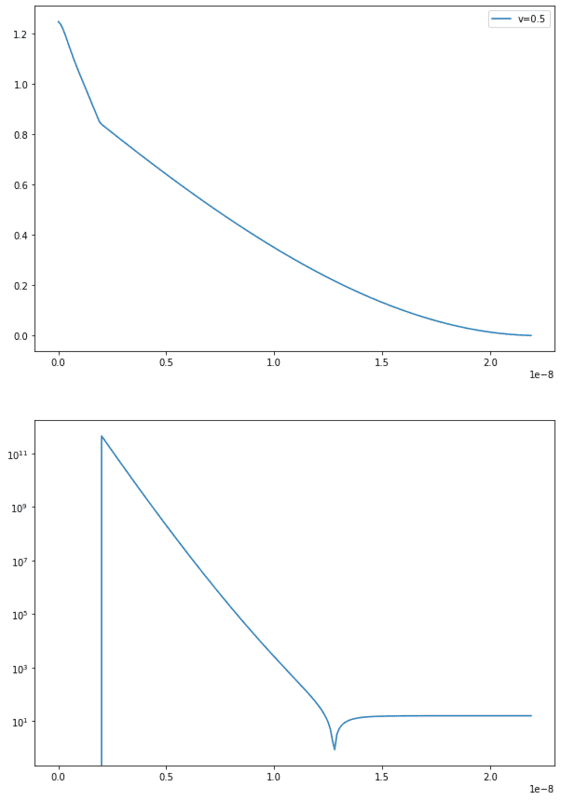
After the oxide-silicon interface at x_ox = 2nm, φ decreases very slowly and doesn't reflect the depletion region. I think that there is a problem with the boundary conditions which are for the moment (with V = 0.5 applied gate voltage in the image):
φ(0) = V - Φm + Φs
with Φm beeing the workfunktion of Al and Φs = χ_si + Eg_si/2 + kb [eV]*T*log(Na/ni)
φ(x_bulk) = 0
I used eps_Si and eps_SiO2 in the box integration for the area of the semiconductor and the oxide. (T = 300 K)
I also tried some variations adding φ_bi (built-in potential) to the boundaries. Could someone please help me and tell me where my mistake is? Is there an interface condition at the SiO2 - Si interface I need to apply?
Thank you very much!
I'm currently working on a 1D Poisson Solver for a MOS device (Al-Si-SiO2). Therefore, I programmed a Poisson Solver which is appling a boxintegration (Finite Volume Method) through the structure from φ(0) at the metal-oxide interface and φ(x_bulk = 20 nm) in in the silicon bulk. It is solving the equation system numerically with a Newton Solver. The solver is working properly. ρ is calculated through:
ρ = q0 * (Nd - Na - n + p)
with
n = ni * exp(- φ / (kb [eV] * T)) and p = ni * exp( φ/ (kb [eV] * T))
The current solution is for φ (top) and ρ (bottom):
After the oxide-silicon interface at x_ox = 2nm, φ decreases very slowly and doesn't reflect the depletion region. I think that there is a problem with the boundary conditions which are for the moment (with V = 0.5 applied gate voltage in the image):
φ(0) = V - Φm + Φs
with Φm beeing the workfunktion of Al and Φs = χ_si + Eg_si/2 + kb [eV]*T*log(Na/ni)
φ(x_bulk) = 0
I used eps_Si and eps_SiO2 in the box integration for the area of the semiconductor and the oxide. (T = 300 K)
I also tried some variations adding φ_bi (built-in potential) to the boundaries. Could someone please help me and tell me where my mistake is? Is there an interface condition at the SiO2 - Si interface I need to apply?
Thank you very much!