- #1
- 1,104
- 960
Is this an interesting problem what do you think?
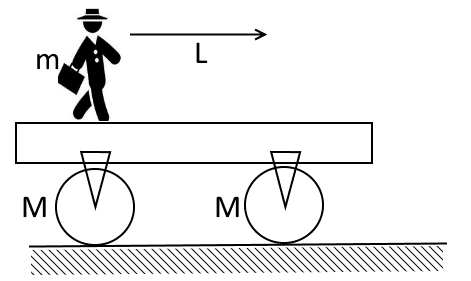
A cart consists of a massless platform and two wheels. Each wheel is a disk of mass M.
The cart stands on a horizontal road and a man of mass m stands upon the platform. Then the man started to go along the cart and after passing the distance L (relatively the cart) he stopped also relatively the cart. The wheels do not slip over the road and there is no friction in the axes.
Which distance the cart passed?
(warning: do not think that the center of mass keeps its position :)
A cart consists of a massless platform and two wheels. Each wheel is a disk of mass M.
The cart stands on a horizontal road and a man of mass m stands upon the platform. Then the man started to go along the cart and after passing the distance L (relatively the cart) he stopped also relatively the cart. The wheels do not slip over the road and there is no friction in the axes.
Which distance the cart passed?
(warning: do not think that the center of mass keeps its position :)