Ackbach said:
Sorry for the delay. This is called $s$-domain circuit analysis. You have the $s$-domain impedances (kinda like what you have in steady-state sinusoidal analysis with phasors):
\begin{align*}
Z_{R}&=R \\
Z_{L}&=Ls \\
Z_{C}&= \frac{1}{Cs}.
\end{align*}
These come straight from the V-I characteristics of resistors, capacitors, and inductors: just LT those relationships, and compare with $V=IZ$, Ohm's Law, to get the $s$-domain impedances (these are defined with the initial conditions zeroed out).
There are tricks for dealing with initial conditions as well - you usually insert a voltage or current source to handle that.
Here is a good summary of the method.
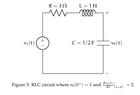
I had the solutions in my office which I retrieved yesterday. It has that
\[
i(t) = \frac{1}{2}\frac{dv_0(t)}{dt}
\]
where does this identity come from? I know we have that \(\dot{v}_0(t) = 2\) but how does that equate to \(2i(t)\)?
Edit 1:
I also worked out \(V_0(s)\) and obtained:
If \(v_i(t) = e^{-3t}\mathcal{U}(t)\), then
\begin{align*}
e^{-3t}\mathcal{U}(t) &= \frac{3}{2}\frac{dv_0(t)}{dt} +
\frac{1}{2}\frac{d^2v_0(t)}{dt^2} + v_0(t)\\
\frac{1}{s + 3} &= \frac{3}{2}(sV_0(s) - v_0(0)) + \frac{1}{2}(s^2V_0(s) -
sv_0(0) - v_0'(0))\\
\frac{2}{s + 3} &= 3sV_0(s) - 1 + s^2V_0(s) - s - 2\\
V_0(s)(s^2 + 3s) &= \frac{2}{s + 3} + s + 3\\
V_0(s) &= \frac{2}{(s + 3)(s^2 + 3s)} + \frac{s + 3}{s^2 + 3s}\\
&= \frac{2 + (s + 3)^2}{s(s + 3)^2}\\
&= \frac{2 + s^2 + 6s + 9}{s(s + 3)^2}\\
&= \frac{s^2 + 6s + 11}{s(s + 3)^2}
\end{align*}
but the solution says that answer is
\[
\frac{2(s^2 + 5s + 7)}{(s + 1)(s + s)(s + 3)}.
\]
Is the solution wrong? I don't see how we can get that.