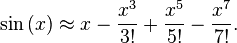Solving trig/algebric equations

[eptheta]

I was finding areas between random lines to pass time when i encountered an equation i could not solve...

7sin(x)=x+1

Do i have to replace sin(x) with the taylor series equivalent

Or is there another way to solve it ?

Thank you.

 

[Mentallic]

You can only get an analytical solution at best, i.e. a good approximation for x.

 

[eptheta]

You can only get an analytical solution at best, i.e. a good approximation for x.

Sure, I'm looking for a good approximation... Would it involve plotting the function f(x)=7sin(x)-x-1 on a graph and picking points on the x-axis or is there a mathematical method to solve something like this...

How would you solve it ?

 

[Mentallic]

Oh ok as long as we're clear we can't solve this algebraically

Yes you would use the function f(x)=7sin(x)-x-1 and to find a good approximation for this function, I'd probably use "[URL method[/URL].

 

[eptheta]

Unfortunately I don't really know what to do to solve it... Could you solve this specific example using Newton's method ?
If it is too long, then perhaps you could get me started in the right direction (the Wikipedia article fried my brain, I'm not even in college...)

Thank you.

 

[Mentallic]

Yes it definitely works for this problem.

It is defined as follows:

x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}

x_n is your first estimated solution, and then x_{n+1} will be your next more closely approximated solution (as long as you use a value of x that is close enough to the actual value).

Now, f(x)=7sinx-x-1 has 5 real roots so depending on which root you're looking for, choose an x that is quite close to it to begin with. Keep applying Newton's method and it should give you a very good approximation pretty quickly.

 

[eptheta]

Wow ! That was fast... Thanks a lot !
I have one more question though...

I used Newton's method for some random polynomials like x³+4x²-3x+4=0 (easily done on a calculator, but this was more fun) keeping my x_n as 0...
Finding my first value (x=-4.8) I used long division to divide my expression by (x+4.8) and then used Newton's method for the remaining polynomial, thus finding all the 3 factors of the expression...

However, I am confused when it comes to my previous function...
How do i get all 5 values of x for f(x)=7sin(x)-x-1 ?
Do I use Newton's method to find the first factor and then change my f(x) to:
f(x)=(7sin(x)-x-1)/(x-a) [where a is the first factor i get]
and then use the method again and again...

I have not tried this yet because differentiating it will become progressively more painful...
Will this work and/or is there any other way to get all 5 factors ?

Thanks

 

[Mentallic]

You couldn't have found the other factors of that cubic... you divided by an approximation for the real root. x\approx -4.8 but really, the exact value of x is irrational and expressing it is complicated.
For example, say we have the function y=x-1, if we divide that by x-(1+0.001) then we now have some rational function which still has a root of 1 and instead now has a vertical asymptote at x=1+0.001.

Since your equation is mixed with trig and algebra, we can't solve the roots algebraically so the best we can do is get a good approximation, which means we can't divide by the root in order to simplify the expression.

The best way would probably be to use a graphing calculator or a carefully drawn diagram of the functions y=7sin(x) and y=x+1 to give yourself a good starting point to find where the roots lie approximately, at which point you can use Newton's method again.

 

[eptheta]

Darn, that's too bad, I'm never too good with graphic approximations...

Is there a threshold range for which Newton's method will return a particular value of x?
That is, if f(x)=sin(x), what is the range of values for x_n for which Newton's method will give me x=0 and not jump to x=+\pi or x=-\pi

Is there a derivation for this range based on the function f(x) ?

Thanks

 

[eptheta]

Mentallic? have any idea how close the first approximation needs to be to the actual value to get the correct one ?

 

[Mentallic]

Darn, that's too bad, I'm never too good with graphic approximations...

If you haven't got a graphing calculator handy and just have no chance of getting a decent approximation by hand-drawing it, you can use the intermediate value theorem. This is pretty simple. Say you have y=x²-2 and want to find where y=0, thus x=sqrt(2), by your graph you estimate it is between 1 and 2, checking to make sure, you find the value of y at x=1, f(1) and notice that it is less than zero, so you check f(2) and notice it is more than zero. So this means the root is somewhere in between x=1 and x=2, take x=1.5, it is slightly more, so take x=1.25, slightly less... so take half way between 1.25 and 1.5.. etc. It's a slow process but it will give you a good head start to kick off your Newton's method approximation.

Is there a threshold range for which Newton's method will return a particular value of x?
That is, if f(x)=sin(x), what is the range of values for x_n for which Newton's method will give me x=0 and not jump to x=+\pi or x=-\pi

Is there a derivation for this range based on the function f(x) ?

Thanks

I don't believe there is. The way Newton's method works is that with your first approximation, it finds where the function actually is at that x value, and then calculates the x value of the tangent line that cuts the x-axis. This is the next approximation and it just keeps doing this over and over.
Say for sin(x), if you take x=\pi/4\approx0.78 as your first approximation, then Newton's will bring back the value x=\pi/4-1\approx -0.21 and it is clear that since the second value brought back something closer to the true root, it will converge to x=0. If you took say x=\pi/2-0.001 then the tangent line from this point is nearly flat so it will reach a very long distance before touching the x-axis again to give the next approximation. Your next value would be x\approx -998 so obviously you're screwed here. But you can even take x=4.5 and return x=-0.1 so yeah, just keeping the rule of thumb that you need a decent first approximation will come in handy. It really depends on the function too,

say, you want to find the root x=0 of y=x^{1/3} then applying Newton's method: x_{n+1}=x_n-\frac{x_n^{1/3}}{\frac{1}{3}x_n^{-2/3}}=x_n-3x_n=-2x_n So whatever first value you use, the next will always double and become negative of it, thus never converging to 0.