Spaceship approaching Mars and relative motion

[Like Tony Stark]

Homework Statement

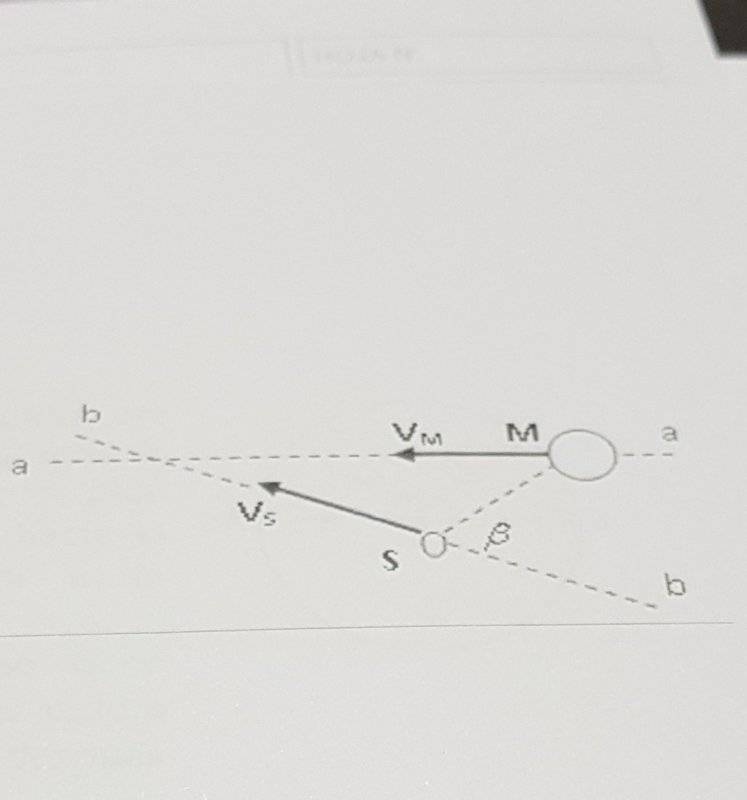
The spaceship S approaches Mars following the trajectory $b-b$ with velocity $\vec v_S=19.3 \frac{km}{s}$ with respect to the Sun. If Mars has a velocity $\vec v_M=24.1 \frac{km}{s}$ along the trajectory $a-a$ with respect to the Sun, determine the angle between $SM$ and $b-b$ such that a person inside the spaceship "sees" that Mars is moving towards him.

Relevant Equations

$\vec v_{B/A}=\vec v_B - \vec v_A$

As the problem asks for the spaceship's perspective, I know that I should take $\vec v_S=0$ and $\vec v_M=24.1-19.3$ because the motion is relative to the spaceship. Then, the relative velocity of Mars and $SM$ should have the same direction. If they have the same direction, that angle would be 90°, wouldn't it? I mean, probably I'm forgetting something, but that's the way I tried to do it

 

[RPinPA]

I know that I should take $\vec v_S=0$ and $\mathbf{\vec v_M=24.1-19.3}$ because the motion is relative to the spaceship.

The equation for $\vec v_M$ is a vector equation. So on the right hand side should be a vector subtraction. You have treated them as scalars.