Destroxia
- 204
- 7
1. Homework Statement
Why does the non-relative simultaneous frame have an additional term of ##v \Delta t## along with the contracted length ## L ## for ## \Delta x ##?
2. Homework Equations
## L + v \Delta t = \Delta x ## ---- (1)
## \Delta x = \gamma \Delta x' = \gamma L_{\star} ## ---- (2)
3. The Attempt at a Solution
What I understand:
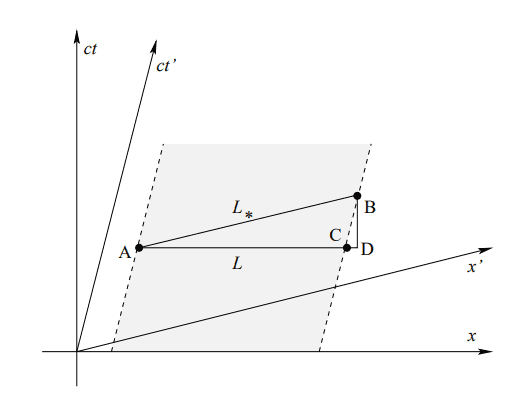
I understand why Length AB within the above diagram is ## L_{\star} ## (Proper Length), it is because that frame is moving with the object (ct', x'), and thus the object appears to be still, and the measurement for the distance shouldn't change if you are still with the object. I understand that AD is ## \Delta x ## in the rest frame (ct, x), and that DB is ## c \Delta t ## in the rest frame (ct, x), as well.
What I don't understand:
What I am not understanding in the least, is the AC section... How is that ## L ## (Contracted Length)? Shouldn't contracted length just be whatever the rest observer is seeing (i.e. The length AD)? Why is the rest observer seeing the contracted length AC, with C along the world line of B? What exactly is CB? I know the object appears to be moving distance ## v \Delta t ##, so that's what CD is, but I still can't see why the new length ## L ## isn't AD, and not AC.
Why does the non-relative simultaneous frame have an additional term of ##v \Delta t## along with the contracted length ## L ## for ## \Delta x ##?
2. Homework Equations
## L + v \Delta t = \Delta x ## ---- (1)
## \Delta x = \gamma \Delta x' = \gamma L_{\star} ## ---- (2)
3. The Attempt at a Solution
What I understand:
I understand why Length AB within the above diagram is ## L_{\star} ## (Proper Length), it is because that frame is moving with the object (ct', x'), and thus the object appears to be still, and the measurement for the distance shouldn't change if you are still with the object. I understand that AD is ## \Delta x ## in the rest frame (ct, x), and that DB is ## c \Delta t ## in the rest frame (ct, x), as well.
What I don't understand:
What I am not understanding in the least, is the AC section... How is that ## L ## (Contracted Length)? Shouldn't contracted length just be whatever the rest observer is seeing (i.e. The length AD)? Why is the rest observer seeing the contracted length AC, with C along the world line of B? What exactly is CB? I know the object appears to be moving distance ## v \Delta t ##, so that's what CD is, but I still can't see why the new length ## L ## isn't AD, and not AC.