Special Relativity Paradox "Terrorist and Spaceship"

[sergiokapone]

The ship left Earth at a speed of 0.5c . When the distance between the ship and Earth was 0.25 light year, a terrorist was caught on Earth who said that he had planted a bomb at the time of departure and activated it for 10 months. At that moment, a warning signal was sent from Earth.

The diagram looks like this

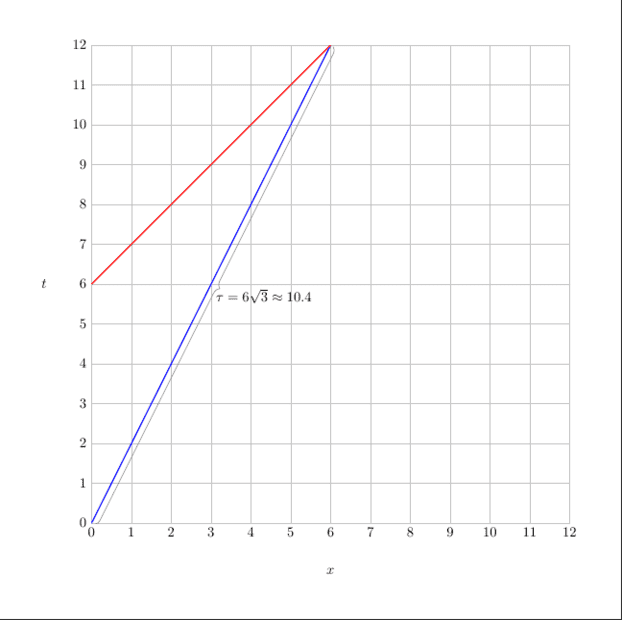
According to the ship's clock, $$\tau = 12\cdot \sqrt{1- \left(\frac12\right)^2} \approx 10.4 $$months have passed, so the ship must explode.

The question is this. What would the diagram look like in the ship's frame of reference? The ship is already stationary and the earth is traveling at $-0.5c$.

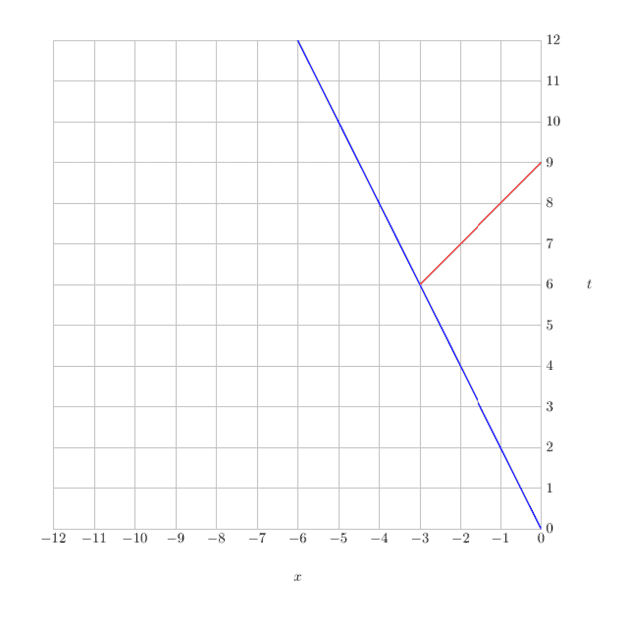
This diagram contains an error, according to the previous diagram, there should be 10.4 months, but this one shows 9 months. I must have forgotten something and forgot to account for it. How to draw the diagram correctly from the ship's point of view?

 

[Dale]

I must have forgotten something and forgot to account for it.

It is almost always the relativity of simultaneity. The message is not sent at $t=6$ in the ship frame.

 

[PeterDonis]

When the distance between the ship and Earth was 0.25 light months

"When" according to what frame? Distance according to what frame? These things always need to be specified in an relativity scenario.

 

[sergiokapone]

It is almost always the relativity of simultaneity. The message is not sent at $t=6$ in the ship frame.

Yes, I understand that by the ship's clock it will not be $6$ months, but what about the distance, it will be $3$ light months from the ship's point of view (or not?). What will the diagram look like?

 

[sergiokapone]

"When" according to what frame? Distance according to what frame? These things always need to be specified in an relativity scenario.

According to Earth. That's where my gap is, relative to the ship, would that be a different distance?

 

[Ibix]

Plug in the Lorentz transforms. The signal is sent at $x=0, t=6$ (assuming your diagram is correct and the description should say 0.25 light years) and received at $x=6, t=12$. Lorentz transform those events. Job done.

 

[Dale]

Yes, I understand that by the ship's clock it will not be $6$ months, but what about the distance, it will be $3$ light months from the ship's point of view (or not?). What will the diagram look like?

It will not be 3 light-months. It will be $0.5 t \mathrm{\ light months}$ where $t$ is the time that it is sent in the ship's frame.

 

[Nugatory]

Yes, I understand that by the ship's clock it will not be $6$ months, but what about the distance, it will be $3$ light months from the ship's point of view (or not?). What will the diagram look like?

What are the coordinates of the "message sent" event , using the frame in which the earth is at rest?
(Your first diagram shows them as $x=0$ and $t=6$, not consistent with the text above it).

Use the Lorentz transformations to find the coordinates of that event using the frame in which the ship is at rest. That will give you the correct starting point for the line indicating the path of the warning message in the second disgram, the one drawn using coordinates n which the ship is at rest.

 

[PeterDonis]

relative to the ship, would that be a different distance?

Yes. But the event of the warning being sent from Earth will also occur at a different time in the ship's frame, as has already been pointed out.

 

[sergiokapone]

I'll summarize. Thank you to everyone who responded and helped me.

 

[sergiokapone]

 

[robphy]

Note that the Doppler factor for $v/c=0.5$ is $k=\sqrt{\frac {1+v/c}{1-v/c}}=\sqrt{3}$, which is about 10.39/6.

By the way, once you know 10.39 is the wristwatch time of the receiver when the signal received,
in your receiver frame, you can draw a past-directed light signal from 10.39 on the receiver worldline.. and locate the intersection event with the source worldline.