- #1
Lluis Olle
- 131
- 33
- TL;DR Summary
- I'm trying to express a solution to the twin paradox, without resorting too much to Minkowski diagrams, lines of simultaneous events and all that stuff, considering a constant |g| acceleration round trip. Is this solution of the twin paradox correct from the S-R point of view, considering a constant |g| round trip?
Applying the Lorentz transformation to velocity and acceleration, we can easily obtain that Aγ3 = α, where A is the acceleration measured by the stationary observer and α is the proper acceleration of the relative moving object. From this point, the equations for a constant accelerated motion can also be obtained. Is important to remark that such equations are directly derived from the Lorentz transformation itself, and so is a consequence in S-R.
In S-R, constant accelerated motion is then described in the spacetime diagram by a hyperbolic worldline.
In layman's terms this makes sense, because if the speed of light were not invariant, then the accelerated worldline would be a parabola... but then in S-R this is not possible because the c-speed limit, so a hyperbolic worldline, asymptotically converging to the c-speed, is easy to understand and visualize.
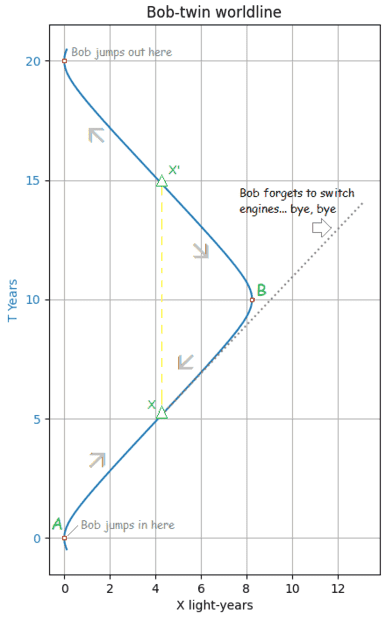
Now, imagine a spaceship that has a proper acceleration of |1g|. It comes from far, far away..., and just passes by an Earth space station with zero relative speed at that position (A). Bob-twin takes advantage of this event and promptly jumps into the spaceship, that continues with its |1g| acceleration moving away from Earth.
The trajectory of the spaceship runs far away from any massive object, and the only interest of Bob-twin is to check some S-R predictions, with its Casio© G-atomic clock in his wrist, which was a gift from his Alice-twin sister at their last mutual birthday.
At a certain intermediate position (X), the spaceship stops its rear engine, fires the front engine, and begins to slow down (relative to Earth) at |1g|. Let the proper time measured at the spaceship be τx when the switching occurs.
At some position later (B), the relative speed with Earth will be zero again. From the Earth observer, this event happens at (TB,XB), and for Bob-twin his clock reads τB when he observes such event. There's no need to be very precise with the timings, give or take a few hours.
Then, the spaceship begins moving towards Earth, always at |1g|, until a certain intermediate position is reached, at which the spaceship turns off its front engine, fires the rear engine, and begins to slow down (relative to Earth) at |1g|. When the spaceship reaches more or less the starting position (relative speed to Earth: zero), Bob-twin jumps off this spaceship, and is recovered by another, that brings him safely to Earth.
It's important to remark that the spaceship is always moving with a proper acceleration magnitude of 1g. Always!
Then, using the hyperbolic motion coordinate equations, we can derive easily the following conditions that have to be true at the event of switching the engines at proper time τx, taking into account that the spaceship will be at event (TB,XB) sometime later, as its motion continues afterwards the switching event with |1g| acceleration:
##\frac{c^2}{g} \cdot \cosh{(\frac{g \cdot \tau_x}{c})}=X_B-\frac{c^2}{g} \cdot \left[\cosh{(\frac{g \cdot (\tau_x - \tau_B)}{c})}-1\right]##
##\frac{c^2}{g} \cdot \sinh{(\frac{g \cdot \tau_x}{c})}=cT_B + \frac{c^2}{g} \cdot \sinh{(\frac{g \cdot (\tau_x - \tau_B)}{c})}##
##\tanh{(\frac{g \cdot \tau_x}{c}})=\tanh{(\frac{g \cdot (\tau_B - \tau_x)}{c}})##
Solving the system, we can get the corresponding τx, τB and XB for a given TB time in Earth:
Let's say that TB is 10 Years at Earth, so Alice-twin is about 20 years older now. Solving the equations, the total elapsed proper time τ in the spaceship is about 9.088 Years (is the reading of the Bob-twin atomic-clock elapsed time), and so Bob-twin has aged about 9 years, and the spaceship has traveled 8.246+8.246 light-years round trip.
So Alice-twin argues with Bob-twin: I missed you birthday's gift 9 times in a row, but you missed mine 20 times, so you owe me 11 gifts. Bob-twin obviously disagrees.
(As I have a lot of problems with LaTex in PF, I also attach an image of the equations, in case of...).
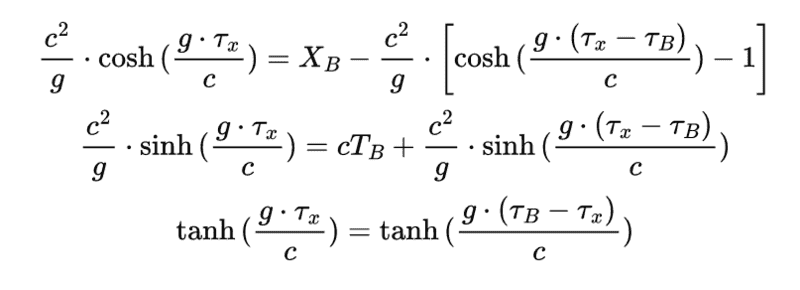
In S-R, constant accelerated motion is then described in the spacetime diagram by a hyperbolic worldline.
In layman's terms this makes sense, because if the speed of light were not invariant, then the accelerated worldline would be a parabola... but then in S-R this is not possible because the c-speed limit, so a hyperbolic worldline, asymptotically converging to the c-speed, is easy to understand and visualize.
Now, imagine a spaceship that has a proper acceleration of |1g|. It comes from far, far away..., and just passes by an Earth space station with zero relative speed at that position (A). Bob-twin takes advantage of this event and promptly jumps into the spaceship, that continues with its |1g| acceleration moving away from Earth.
The trajectory of the spaceship runs far away from any massive object, and the only interest of Bob-twin is to check some S-R predictions, with its Casio© G-atomic clock in his wrist, which was a gift from his Alice-twin sister at their last mutual birthday.
At a certain intermediate position (X), the spaceship stops its rear engine, fires the front engine, and begins to slow down (relative to Earth) at |1g|. Let the proper time measured at the spaceship be τx when the switching occurs.
At some position later (B), the relative speed with Earth will be zero again. From the Earth observer, this event happens at (TB,XB), and for Bob-twin his clock reads τB when he observes such event. There's no need to be very precise with the timings, give or take a few hours.
Then, the spaceship begins moving towards Earth, always at |1g|, until a certain intermediate position is reached, at which the spaceship turns off its front engine, fires the rear engine, and begins to slow down (relative to Earth) at |1g|. When the spaceship reaches more or less the starting position (relative speed to Earth: zero), Bob-twin jumps off this spaceship, and is recovered by another, that brings him safely to Earth.
It's important to remark that the spaceship is always moving with a proper acceleration magnitude of 1g. Always!
Then, using the hyperbolic motion coordinate equations, we can derive easily the following conditions that have to be true at the event of switching the engines at proper time τx, taking into account that the spaceship will be at event (TB,XB) sometime later, as its motion continues afterwards the switching event with |1g| acceleration:
##\frac{c^2}{g} \cdot \cosh{(\frac{g \cdot \tau_x}{c})}=X_B-\frac{c^2}{g} \cdot \left[\cosh{(\frac{g \cdot (\tau_x - \tau_B)}{c})}-1\right]##
##\frac{c^2}{g} \cdot \sinh{(\frac{g \cdot \tau_x}{c})}=cT_B + \frac{c^2}{g} \cdot \sinh{(\frac{g \cdot (\tau_x - \tau_B)}{c})}##
##\tanh{(\frac{g \cdot \tau_x}{c}})=\tanh{(\frac{g \cdot (\tau_B - \tau_x)}{c}})##
Solving the system, we can get the corresponding τx, τB and XB for a given TB time in Earth:
Let's say that TB is 10 Years at Earth, so Alice-twin is about 20 years older now. Solving the equations, the total elapsed proper time τ in the spaceship is about 9.088 Years (is the reading of the Bob-twin atomic-clock elapsed time), and so Bob-twin has aged about 9 years, and the spaceship has traveled 8.246+8.246 light-years round trip.
So Alice-twin argues with Bob-twin: I missed you birthday's gift 9 times in a row, but you missed mine 20 times, so you owe me 11 gifts. Bob-twin obviously disagrees.
(As I have a lot of problems with LaTex in PF, I also attach an image of the equations, in case of...).