It depends on what P is. I assume that k is a constant. Otherwise, you have a fourth-order, non-homogeneous ODE.Andreol263 said:Hello guys, I'm studying from Green's Function With Applications by Duff, and he finds the general solution(homogeneous sol.) to this differential equation: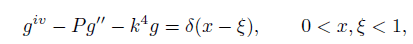, but i I've never seen a equation like this before, how can i manage to solve this equation??
If P is a function of x, what sort of function is it? The general method of solution to these types of ODEs is by infinite series.Andreol263 said:
A special second order ordinary differential equation is a type of differential equation that involves only the first and second derivatives of a single variable. It is typically written in the form y'' = f(x, y, y'), where y' is the first derivative and y'' is the second derivative.
There are various methods for solving a special second order ordinary differential equation, such as the method of undetermined coefficients, the method of variation of parameters, and the method of reduction of order. The specific method used will depend on the form of the equation and the initial conditions.
Special second order ordinary differential equations are commonly used in physics, engineering, and other fields to model systems that involve acceleration, such as motion of objects and oscillations. They can also be used in chemical reactions and other natural phenomena.
Yes, a special second order ordinary differential equation can have multiple solutions. This is because there are typically two arbitrary constants that can be adjusted to produce different solutions. The specific solutions will depend on the initial conditions given for the equation.
A special second order ordinary differential equation is a specific type of second order ordinary differential equation that has the form y'' = f(x, y, y'). In a general second order ordinary differential equation, the coefficients of the derivatives may vary and there may be additional terms involving higher derivatives or other variables. Special second order equations are often easier to solve than general second order equations due to their simpler form.