Discussion Overview
The discussion revolves around the dynamics of a car rolling down a gently sloped hill, specifically a 5% grade over a distance of 200 miles. Participants explore questions regarding the maximum speed the car can achieve, the factors influencing this speed, and whether mechanical limitations might prevent the car from reaching the bottom of the hill.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants question whether the maximum speed will be reached at the bottom of the hill or earlier, suggesting that mechanical features of the car could limit speed.
- Others propose that rolling resistance and aerodynamic drag are critical factors in determining the car's maximum speed.
- One participant emphasizes the need for specific details about the car, such as tire type and pressure, to accurately assess the situation.
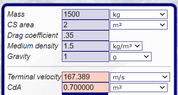
- Another participant calculates potential forces acting on the car, estimating a terminal speed based on various assumptions about drag and resistance.
- Concerns are raised about the complexity of the problem, with some suggesting that the discussion could be simplified unless necessary complexity is warranted.
- A few participants engage in back-and-forth corrections regarding calculations and assumptions, indicating uncertainty about the values used in their models.
Areas of Agreement / Disagreement
Participants express differing views on whether the original question is primarily a physics or automotive issue. There is no consensus on the maximum speed reached or the factors that would influence it, as multiple competing models and assumptions are presented throughout the discussion.
Contextual Notes
Participants highlight the importance of various assumptions, such as the car's weight, drag characteristics, and environmental factors, which remain unresolved. The discussion also touches on the implications of a very long hill, suggesting that the length may not significantly affect the outcome under certain conditions.