Spherical ball rolling on a concave surface

[Tanya Sharma]

Homework Statement

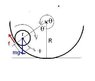
A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R .It makes small oscillations about the lowest point.Find the time period.

Ans : 2∏\sqrt\frac{7(R-r)}{5g}

Homework Equations

The Attempt at a Solution

We displace the spherical ball towards right so that it rolls down towards the bottommost position .

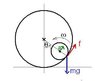
Let the origin be fixed at the CM of the ball and fix coordinate axis with + x-axis rightwards upwards

Let θ be the angle which the CM of the ball makes with the center of the concave surface
Let ∅ be the angle which the ball rotates around its axis i.e CM

Let α be the angular acceleration of the CM of the ball around the center of the concave surface
Let β be the angular acceleration of the ball around the CM

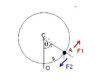
For translation motion of the CM of the spherical ball

f - mgsinθ =ma where a is the acceleration of the CM of the ball

fr = Iβ where I=(2/5)mr²

a=βr (no slip condition)

We also have ,

∅=\frac{R-r}{r}θ

So ,β=\frac{R-r}{r}α

Solving above equations ,I get incorrect answer .

I feel the problem is somewhere with signs .If ,we consider frictional torque around CM as -fr instead as fr or β=-(\frac{R-r}{r})α ,we get correct answer .

How do assign signs to the torque and the angular accelerations just like we assign positive and negative signs to forces and accelerations ?

Kindly help me with the problem .

 

[gurbir14]

Its just that you have a problem with signs in equation for translational motion.

 

[ehild]

When the ball rotates anticlockwise, the CM moves clockwise.

ehild

 

[Tanya Sharma]

Hello ehild

When the ball rotates anticlockwise, the CM moves clockwise.

ehild

Do you mean the direction of angular acclerations α and β are opposite ,and hence a negative sign in the relation β = - (\frac{R-r}{r})α ?

 

[ehild]

It depends what you call alpha and beta. Make a drawing and check all the signs.

ehild

 

[Tanya Sharma]

ehild...I am having trouble assigning signs to rotational quantities angle,torque,angular acceleration ...

In this problem

Let θ be the angle which the CM of the ball makes with the center of the concave surface .When the sphere rolls from rightwards towards bottommost point .θ decreases as motion of CM is clockwise .

Let ∅ be the angle which the ball rotates around its axis i.e CM .∅ increases as ball rotates anticlockwise .

α is the angular acceleration of the CM of the ball around the center of the concave surface .
β is the angular acceleration of the ball around the CM

The magnitude of frictional torque around CM is fr and is anticlockwise .

I am unable to corelate these things .

What decides the frictional torque be fr or -fr ?

I think the direction of α and β is opposite .So should β = -(\frac{R-r}{r})α ??

 

[ehild]

See picture.

The CM moves anticlockwise, Ω=dθ/dt is positive.
Edit: Theta must be the angle indicated in the picture. The correct equation is (R-r)\ddot\theta = mgsin(\theta')-f
instead of

(R-r)\ddot\theta = mgsin(\theta)-f

the friction means a negative torque (rotates the ball clockwise) The angular velocity of the rotation is ω.

\dot\omega = -fr/I

No slip condition: (R-r)Ω+rω=0--> \dot\omega = -\ddot \theta (R-r)/r

ehild

 

[Tanya Sharma]

See picture.

The CM moves anticlockwise, Ω=dθ/dt is positive.

(R-r)\ddot\theta = mgsin(\theta)-f

the friction means a negative torque (rotates the ball clockwise) The angular velocity of the rotation is ω.

\dot\omega = -fr/I

No slip condition: (R-r)Ω+rω=0--> \dot\omega = -\ddot \theta (R-r)/r

ehild

Solving the above equations we get \ddot \theta =\frac{5gsin\theta}{7(R-r)} instead of \ddot \theta = - \frac{5gsin\theta}{7(R-r)}

How are we missing the negative sign ?

The signs of the angular quantities have been really confusing in this problem .

 

[ehild]

How are we missing the negative sign ?

The signs of the angular quantities have been really confusing in this problem .

Well, I succeeded to confuse myself as I drew the ball at negative angle... Now I try to define the positive direction for everything.

So the ball is at positive θ initially. The acceleration is positive if it is up and to the right. The tangential component of gravity acts downward and to the left, so θ will decrease. Without friction, the ball would slide to the left, so static friction acts to the right and up. The static friction yields positive torque with respect to the CM.

ma=f-mgsinθ. a=(R-r)d²θ/dt²

rf=Idω/dt

No-slip condition: v(CM)+rω=0-->dω/dt=-(R-r)/r d²θ/dt²

I hope that is correct now.

ehild

 

[Tanya Sharma]

ehild..Thanks for the response

I have really confused myself to the extreme in this question . :( I will put my doubts here.

The acceleration is positive if it is up and to the right.

ma=f-mgsinθ. a=(R-r)d²θ/dt²

ehild

The acceleration will always be directed towards the bottommost point of the surface that is equilibrium position .So whether the sphere is rolling upwards towards right from mean position or rolling downwards towards mean position ,the sign of a in equation for translation motion should always be negative i.e f-mgsinθ = -ma . Am I right or wrong ?

 

[ehild]

It was the definition of positive directions. I took the acceleration positive if the CM moved anticlockwise. That means, the acceleration has negative value when the ball rolls towards the equilibrium point from that position.

The same as in a Cartesian system of coordinates: you set the x-axis horizontal, positive direction pointing to the right. Then a particle to the right from the origin and moving towards the origin has positive x coordinate and negative velocity v=dx/dt as x decreases during the motion.

The acceleration will always be directed towards the bottommost point of the surface that is equilibrium position .So whether the sphere is rolling upwards towards right from mean position or rolling downwards towards mean position ,the sign of a in equation for translation motion should always be negative i.e f-mgsinθ = -ma . Am I right or wrong ?

You have to define the positive direction both for the angle θ and the acceleration once. The ball oscillates about the equilibrium point. Once it is to the left once it is to the right, but it always accelerates towards the equilibrium. Imagine an SHM along the x-axis around the origin. Once the particle is to the right, once it is to the left from the origin, but always accelerates toward the origin. Do you consider the acceleration always negative?

You can define the positive direction for a anyway, but take care when relating it to the second derivative of the angle θ. If you count the angle anticlockwise from the vertical, V(CM)=-(R-r)dθ/dt, as the angle decreases when the sphere moves to the left, and the acceleration is a=-(R-r)d²θ/dt².

ehild

 

[Tanya Sharma]

It was the definition of positive directions. I took the acceleration positive if the CM moved anticlockwise. That means, the acceleration has negative value when the ball rolls towards the equilibrium point from that position.

The same as in a Cartesian system of coordinates: you set the x-axis horizontal, positive direction pointing to the right. Then a particle to the right from the origin and moving towards the origin has positive x coordinate and negative velocity v=dx/dt as x decreases during the motion.

ehild

How is it possible that f-mgsinθ=ma ,with both f and a positive .As per this equation ,the friction accelerates the ball upwards,which is not possible .

f-mgsinθ = ma is correct ,if we consider a to be an unknown quantity , with unknown direction .

 

[ehild]

How is it possible that f-mgsinθ=ma ,with both f and a positive .As per this equation ,the friction accelerates the ball upwards,which is not possible .

f-mgsinθ = ma is correct ,if we consider a to be an unknown quantity , with unknown direction .

Yes, it is an unknown quantity, with unknown (and changing) direction. And it is related to the angle. The relation must be the same at any position of the ball along its track.
A force with the same direction as f would accelerate the ball upwards, while gravity accelerates it downwards.

ehild

 

[Tanya Sharma]

Do you consider the acceleration always negative?

What I meant was that when we fix rightwards upwards positive ,then irrespective of whether ball rolls upwards or downwards ,f-mgsinθ =-ma ,where we have taken sign of acceleration a into account .i.e downwards in the negative direction.

It was the definition of positive directions. I took the acceleration positive if the CM moved anticlockwise. That means, the acceleration has negative value when the ball rolls towards the equilibrium point from that position.

What do you mean by the above statement ? We generally don't assign positive direction to acceleration but instead fix an axis with positive and negative directions .After that we consider whether acceleration should be positive or negative .Isnt it?

Kindly elaborate more on the relation between acceleration and the angle . I am having difficulty understanding positive and negative angles and how acceleration is related to the angle .

 

[ehild]

Consider a simple circular motion like in the figure. Instead of a linear coordinate x, you give the position of the point along the circle either with arc length s between O and A, or with the angle θ, measured from CO anticlockwise. Note that s and θ serve as coordinates now, both can be either positive and negative.

When the point changes position, the angular displacement is positive if θ increased. The angular velocity is defined as ω=dθ/dt.
ω is positive if θ increases and negative when θ decreases. So the direction of the angular velocity is defined with respect to the anti-clockwise direction.

The linear velocity along the arc of circle is defined as v=rω. Again, it is positive if the point moves in the positive direction (anticlockwise) and negative when it moves to the opposite direction.
The same with the accelerations. The angular acceleration is β=d²θ/dt², the linear acceleration along the arc is a=rβ.

When some force F acts at a point tangent to the circle, it counts positive if its direction is the same as the positive direction along the circle. So F1 causes positive acceleration and F2 causes negative one. But ma=F holds for both forces.
If the magnitude of F1is f, and the magnitude of F2 is mgsinθ, Newton II reads as ma=-mgsinθ+f.

ehild

 

[Tanya Sharma]

Thanks for the wonderful explanation :)

What about the direction of torque and angular acceleration of the ball around its CM ? Since the frictional torque tries to rotate the ball anticlockwise ,sign of torque fr and angular acceleration β will be positive in both the cases i.e when the ball rolls up towards right as well as rolls down towards bottommost point.

Am I correct ?

 

[ehild]

Thanks for the wonderful explanation :)

What about the direction of torque and angular acceleration of the ball around its CM ? Since the frictional torque tries to rotate the ball anticlockwise ,sign of torque fr and angular acceleration β will be positive in both the cases i.e when the ball rolls up towards right as well as rolls down towards bottommost point.

Am I correct ?

Yes, you are right. When the ball rolls upward, it rotates clockwise. its CM decelerates and also its rotation slows down, by the anticlockwise torque.

If it rolls downward, toward the equilibrium position, it rotates anticlockwise. The CM accelerates and rotates faster and faster because of the anticlockwise torque.

The force of static friction is opposite to the component of gravity.

ehild

 

[Tanya Sharma]

ehild...Thanks !

I am really grateful to you for your time and patience in explaining the concepts :)