Spherical Coordinates Integral

[themadhatter1]

Homework Statement

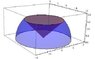
Using spherical coordinates, find the volume of the solid that lies within the sphere x²+y²+z²=4, above the xy-plane and below the cone z=√(x²+y²)

Homework Equations

The Attempt at a Solution

This is what I have so far,

v=\int_{0}^{2\pi}\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\int_{0}^{\frac{2}{cos\phi}}dp d\phi d\theta

However, when evaluating this integral you wind up having an infinite discontinuity between the bounds of the 2nd integral, so you can't evaluate it. Am I thinking of the right shape?

 

[jackmell]

You need to use the right format for the integral:

\int_0^{2\pi}\int_{\pi/4}^{\pi/2}\int_0^{\rho(\phi,\theta)} \rho^2\sin(\phi)d\rho d\phi d\theta

So lemme' ask you this, as you go round it to integrate it, does the upper limit on rho depend on phi or theta?

 

[themadhatter1]

You need to use the right format for the integral:

\int_0^{2\pi}\int_{\pi/4}^{\pi/2}\int_0^{\rho(\phi,\theta)} \rho^2\sin(\phi)d\rho d\phi d\theta

So lemme' ask you this, as you go round it to integrate it, does the upper limit on rho depend on phi or theta?

Oh, haha. Cant believe I forgot that. I would think the upper limit on rho depends on phi because with this shape, you can change theta all you want and rho is not going to change. However, changing phi changes rho, this is because the solid is symmetrical about the z-axis. Right?

 

[jackmell]

Oh, haha. Cant believe I forgot that. I would think the upper limit on rho depends on phi because with this shape, you can change theta all you want and rho is not going to change. However, changing phi changes rho, this is because the solid is symmetrical about the z-axis. Right?

No, changing phi doesn't change the upper limit on rho because you're integrating from zero to the boundary of the sphere right and nothing is getting in the way of rho as it goes from zero to that boundary.

 

[themadhatter1]

Ok, I think I was misinterperting the volume described. I took it to mean basically the shadow cast down by the cone on the xy-plane, since that region lies under the cone, above the xy-plane, and in the sphere. I'm not sure if the area you are thinking of is correct though. In the area you are thinking of part of it doesn't lie under the cone. I think your shape would be a hemisphere with a cone cut out. I was thinking of a cylynder with a cone cut out.

 

[jackmell]

Ok, I think I was misinterperting the volume described. I took it to mean basically the shadow cast down by the cone on the xy-plane, since that region lies under the cone, above the xy-plane, and in the sphere. I'm not sure if the area you are thinking of is correct though. In the area you are thinking of part of it doesn't lie under the cone. I think your shape would be a hemisphere with a cone cut out. I was thinking of a cylynder with a cone cut out.

Ok, now you got me confussed. I'm sayin':

\text{my blue volume}=\int_{0}^{2\pi}\int_{\pi/4}^{\pi/2}\int_0^2 \rho^2 \sin(\phi)d\rho d\phi d\theta

 

[themadhatter1]

Ok, now you got me confussed. I'm sayin':

\text{my blue volume}=\int_{0}^{2\pi}\int_{\pi/4}^{\pi/2}\int_0^2 \rho^2 \sin(\phi)d\rho d\phi d\theta

Hmm, that's what I thought you were thinking. I handed in the assignment today and got the answer key. They setup the integral the way you did in the answer key. However, I would argue that part of the region in that integral is not under the cone. Everything under the cone is contained within a cylinder of r=√(2) centered about the z-axis. Clearly, part of the region is not under the cone. This problem came from Stewart's calculus. At the very least Stewart was unclear, (which wouldn't be the first time). I'll see what my professor has to say.

 

[jackmell]

Hmm, that's what I thought you were thinking. I handed in the assignment today and got the answer key. They setup the integral the way you did in the answer key. However, I would argue that part of the region in that integral is not under the cone. Everything under the cone is contained within a cylinder of r=√(2) centered about the z-axis. Clearly, part of the region is not under the cone. This problem came from Stewart's calculus. At the very least Stewart was unclear, (which wouldn't be the first time). I'll see what my professor has to say.

You got that wrong dude. The cone goes up higher than the sphere and the problem explicitly stated the volume in the sphere under the cone. The way you thinkin' of it would be to say, "the volume under the cone within the sphere where the cone intersects the sphere."