amjad-sh
- 240
- 13
sorry I am going slightly off the topic. <<Moderator's note: split off from this thread.>>
I asked this question because I'm studying a paper concerning the presence of spin orbit coupling at the interface between two metals.
This is the part of the paper I'm studying:
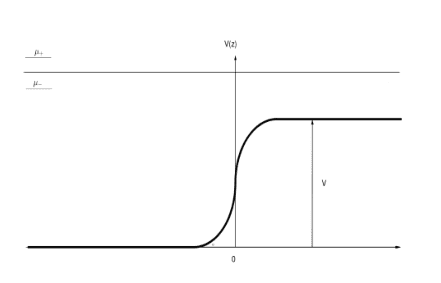
"Our aim is to describe a ballistic spin transport across the interface between two different metals. To simplify calculations and emphasize the physical picture we consider the simplest possible “minimal” model that captures the most important physical aspects of the effects of interest. We model our system as a free electron gas (jellium model) in the presence of a potential forming a step at the interface located at z = 0 (see Fig. 1). The potential step represents different work functions of the two metals. The system is assumed to be translation invariant in the x-y plane. The presence of the interface (the potential step) breaks the inversion symmetry and generates a local SOC term which is responsible for the transport phenomena that we will study later on. The model is described by the following Hamiltonian:
##\mathbf H= \mathbf P^2/2m -\frac {\partial ^2} {\partial z^2}/2m +\mathbf V(z) +\gamma \mathbf V'(z)(\mathbf z \times \mathbf p)\cdot \mathbf \sigma##
where p is the two-dimensional momentum in the x-y plane, V (z) the potential step, σ is a vector of Pauli matrices, and γ is a material dependent parameter which describes the strength of SOC at the interface. The first two terms of the Hamiltonian describe the kinetic energy of the electrons, the third one represents the potential step due to the different work functions, and the fourth term localized at the interface corresponds to SOC due to the gradient of this potential barrier, the ISOC. Because of the translation invariance in the x-y plane the eigenfunctions read ##\psi_{\mathbf p,k}(\mathbf r,z)=e^{i\mathbf p \cdot \rho}\phi_z(k)##, (2) where ρ = (x,y) is the in-plane coordinate, and##\phi_z(k)## are spinor scattering states in z-direction which are labeled by the wave vector k of the incoming wave"
 .
.
I want just to be sure if I understanded the model.
1- The Hamiltonian here is the Hamiltonian of one electron moving in either one of the two metals.
2- any electron moving in the metal will face the same potential V(z), the potential in the both of the metals is constant or periodic, and because of this spin orbit coupling doesn't occur inside the metal ( is this right?) does absence of inversion symmetry renders potential inside the metal nonperiodic?
3-The eigenfunctions of the Hamiltonian are written like this ##\psi_{\mathbf p,k}(\mathbf r,z)=e^{i\mathbf p \cdot \rho}\phi_z(k)## where the x and y components are considered as plane waves and the z component is the only component that contributes in the scattering at the interface.
I asked this question because I'm studying a paper concerning the presence of spin orbit coupling at the interface between two metals.
This is the part of the paper I'm studying:
"Our aim is to describe a ballistic spin transport across the interface between two different metals. To simplify calculations and emphasize the physical picture we consider the simplest possible “minimal” model that captures the most important physical aspects of the effects of interest. We model our system as a free electron gas (jellium model) in the presence of a potential forming a step at the interface located at z = 0 (see Fig. 1). The potential step represents different work functions of the two metals. The system is assumed to be translation invariant in the x-y plane. The presence of the interface (the potential step) breaks the inversion symmetry and generates a local SOC term which is responsible for the transport phenomena that we will study later on. The model is described by the following Hamiltonian:
##\mathbf H= \mathbf P^2/2m -\frac {\partial ^2} {\partial z^2}/2m +\mathbf V(z) +\gamma \mathbf V'(z)(\mathbf z \times \mathbf p)\cdot \mathbf \sigma##
where p is the two-dimensional momentum in the x-y plane, V (z) the potential step, σ is a vector of Pauli matrices, and γ is a material dependent parameter which describes the strength of SOC at the interface. The first two terms of the Hamiltonian describe the kinetic energy of the electrons, the third one represents the potential step due to the different work functions, and the fourth term localized at the interface corresponds to SOC due to the gradient of this potential barrier, the ISOC. Because of the translation invariance in the x-y plane the eigenfunctions read ##\psi_{\mathbf p,k}(\mathbf r,z)=e^{i\mathbf p \cdot \rho}\phi_z(k)##, (2) where ρ = (x,y) is the in-plane coordinate, and##\phi_z(k)## are spinor scattering states in z-direction which are labeled by the wave vector k of the incoming wave"
I want just to be sure if I understanded the model.
1- The Hamiltonian here is the Hamiltonian of one electron moving in either one of the two metals.
2- any electron moving in the metal will face the same potential V(z), the potential in the both of the metals is constant or periodic, and because of this spin orbit coupling doesn't occur inside the metal ( is this right?) does absence of inversion symmetry renders potential inside the metal nonperiodic?
3-The eigenfunctions of the Hamiltonian are written like this ##\psi_{\mathbf p,k}(\mathbf r,z)=e^{i\mathbf p \cdot \rho}\phi_z(k)## where the x and y components are considered as plane waves and the z component is the only component that contributes in the scattering at the interface.
Attachments
Last edited by a moderator: