Stability of Droplet Climbing on a Needle with Varying Contact Angle

[chingel]

TL;DR Summary

Will a droplet forming at the end of the needle start climbing up the outer side of the needle to keep its contact angle? What shape will it form?

Let's say we are pushing water down a needle, the contact angle between the needle and the water is $\mathrm{45°}$.
For simplicity let's assume there is no gravity.

As the water is initially moving down in the left image, the angle $\theta=\mathrm{45°}$ and the surface of the water is a part of a sphere with some fixed radius.

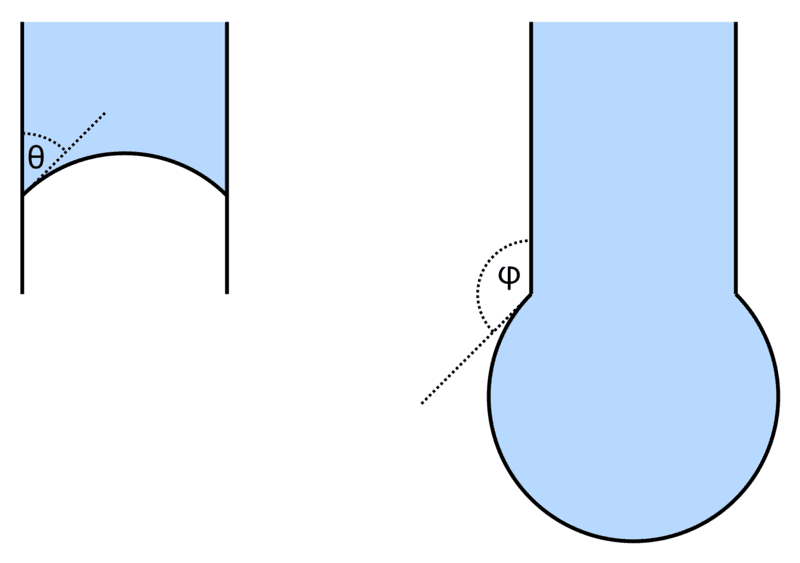
When the water moves to the end of the needle, we have $\varphi=\mathrm{315°}$. As we push more water out, $\varphi$ keeps decreasing and the surface should always be a part of a sphere (or flat when $\varphi=\mathrm{270°}$).

I would think that the droplet volume grows until it reaches the contact angle with the outer side of the needle (i.e. $\varphi=\mathrm{135°}$ in the figure on the right), and then I think the liquid should start moving up the outer side of the needle, since the contact line will be pulled up to keep the contact angle?

Since there is only one specific radius for a sphere with the given contact angle all around the needle, it seems the surface can't stay a sphere, contain more water and keep the $\mathrm{45°}$ contact angle at the same time, so what will it do if we push more water out?

 

[Andy Resnick]

[This question let's me use one of my favorite words...]

They way you structured the problem, the water will also wet the outer surface of the needle and so as the drop volume increases, the contact line will move and the droplet shape will be a sphere-ish shape (owing to gravitational deformation) until the mass of the drop can no longer be supported by the contact line tension, and a droplet will detach.

If, on the other hand, the contact line is pinned to the needle edge, canthotaxis (that's the word!) permits the contact angle to vary all the way to (IIRC) π-θ. The droplet shape is again sphere-ish.

 

[chingel]

Let's assume for simplicity that there is no gravity.

I understand that canthotaxis says that in the figure in the OP on the right $\varphi$ can be between 135 and 315 degrees and the contact line is pinned to the edge of the needle in the whole range. My question is what happens after that, when you push out even more water.

If the contact line moves up and the surface remains a sphere, then the water droplet minus the needle will contain less water, because the sphere radius is fixed by the contact angle condition and now more needle is inside the sphere, so the water volume outside the needle decreases.

I think this means that there will be no one stable shape? That some unknown amount of water will flow up the needle and form a separate wet spot on the outside needle wall and a droplet will remain at the end of the needle with a $\varphi$ at some value over 135 degrees.