Stabilizer Leg Linear Actuator Force to Jack up a Truck's rear tyres

[Ashferico]

Homework Statement

A truck weighing 80kN is supported at its two axles. The truck also carries a load on a lifting arm of 45kN. It has stabilizer legs at the rear of the vehicle. What is the required force of the linear actuators that are driving the stabilizer leg to jack the rear tyres so they are not in contact with the ground?

Relevant Equations

Resultant Torque = Moment of Intertia I x Angular Acceleration

Moment of Inertia I = Mass x (Radius of Gyration)^2

Parallel Axis Theorem: I = I(cm) + md^2

Angular Displacement = 0.5 x Angular Acceleration x (time^2)

Resultant Torque = Sum of Clockwise Moments - Sum of Anticlockwise Moments

Moment = Force x Perpendicular Distance from Pivot

Hi,

I previously posted about the statically indeterminate truck problem. Thank you to everyone who helped me. However, I now realized that isn't the problem I need to solve. I need to know the force of the linear actuators to lift the rear tyres off the ground.

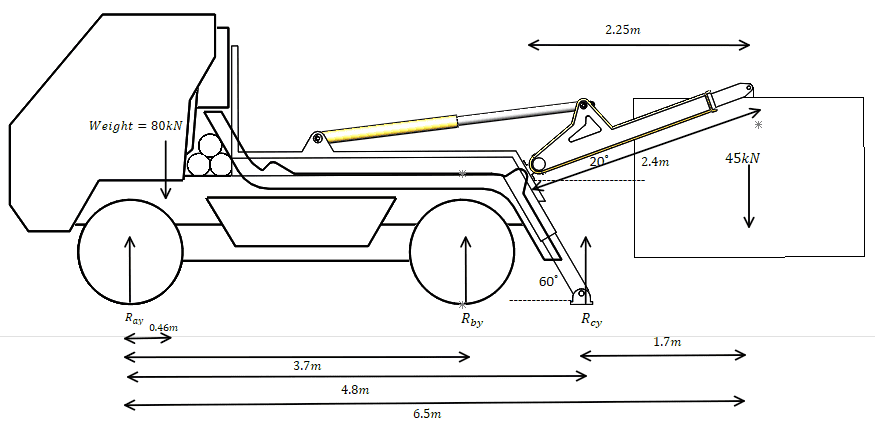
Since the tyres will be lifting off the ground, it can't be in static equilibrium.

If it rotating about the front tyres, then there must be a resultant torque:

Resultant Torque = Moment of Intertia I x Angular Acceleration

If I make the assumption that rear tyres are raised 1cm from the ground:

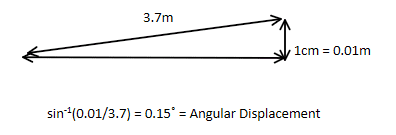
The angular displacement is 0.15 degrees.

If I make the assumption this happens over 5 seconds:

Angular Displacement = 0.5 x Angular Acceleration x (t^2)

Angular Acceleration = 0.012°/s^2 =0.0002 radians/s^2

Now if we use:

Resultant Torque = Moment of Intertia I x Angular Acceleration

&

Resultant Torque = Sum of Clockwise Moments - Sum of Anticlockwise Moments

Moment of Intertia I x (-0.0002) = (80 x 0.46) + (45 x 1.85) - (Rcy x 4.8)

If I calculated the Moment of Inertia of the entire truck and box combined, then I can calculate Rcy.

Is this Rcy, the linear actuator force required by the stabilizer leg to jack the vehicle?

Likewise, how can I calculate the Moment of Inertia of the truck about the front wheel's tyre?

 

[jbriggs444]

Since the tyres will be lifting off the ground, it can't be in static equilibrium.

As long as the stabilizers are extended slowly, it reasonable to assume that a stable static equilibrium exists at all times.

Certainly, that is a desirable state of affairs. You want to be able to stop the stabilizers at any point and not have the rig tip over.

 

[Ashferico]

As long as the stabilizers are extended slowly, it reasonable to assume that a stable static equilibrium exists at all times.

Certainly, that is a desirable state of affairs. You want to be able to stop the stabilizers at any point and not have the rig tip over.

Hi,

Thank you for the reply again. Does that mean the original statically indeterminate calculation was the force required of the linear actuators?

 

[jbriggs444]

Thank you for the reply again. Does that mean the original statically indeterminate calculation was the force required of the linear actuators?

As I recall the original problem had you put down the stabilizer legs until they were just touching the ground. Then you raised the load and asked about the resulting support force from the legs. There was no requirement that the rear wheels be lifted from the ground. That was a difficult situation because lifting the load would raise the chassis somewhat off both front and rear springs. One needed to think about spring constants in order to determine the resulting equilibrium load distribution.

In this case, my understanding is that you have [perhaps foolishly] raised the load first and then put down the stabilizer legs sufficiently to force the rear wheels clear of the ground. This is a much easier problem. There is no need to worry about spring constants. The rear wheels are irrelevant this time. The only support is at the stabilizers and at the front wheels. No extra unknowns to solve for. Easy peazy.

But the two situations are different. Two different problems with two different solutions.

 

[Ashferico]

As I recall the original problem had you put down the stabilizer legs until they were just touching the ground. Then you raised the load and asked about the resulting support force from the legs. There was no requirement that the rear wheels be lifted from the ground. That was a difficult situation because lifting the load would raise the chassis somewhat off both front and rear springs. One needed to think about spring constants in order to determine the resulting equilibrium load distribution.

In this case, my understanding is that you have [perhaps foolishly] raised the load first and then put down the stabilizer legs sufficiently to force the rear wheels clear of the ground. This is a much easier problem. There is no need to worry about spring constants. The rear wheels are irrelevant this time. The only support is at the stabilizers and at the front wheels. No extra unknowns to solve for. Easy peazy.

But the two situations are different. Two different problems with two different solutions.

So, in this scenario. Its just two supports, front wheels and stabilizers. The force of the stabilizer in static equilibrium is also the force to jack the vehicle up? Thus it is the force of the linear actuators? It is for a mechanical design project and I need to specify the right components.