Standing jump on a spring platform

[Bladerunner56]

Hello PF,

I'm looking for physics and math insights that will help me set up and solve a diff. eqn. for the height of a jump from a spring platform. The problem requires a bit of setup explanation, because it appears simple at first, but then, not so simple.

First consider a person standing with knees bent on solid ground. At t=0, the person is at rest. The person then executes a vertical jump by exerting a sinusoidal force to propel the body up. We assume a force amplitude and frequency, and a mass. We'll simplify things by assuming a center of mass (COM) for the person and that the spindly, yet strong legs, have no mass. The position of the COM (initially at a height of 1) begins to move upward immediately and continues to accelerate upward until the force stops or the feet leave the ground. So, at t=0, v, a, and KE = 0, and x=1.

Now consider that the person performs the same jump, but stands on a massless spring platform with spring constant K. Note that this setup is different from most mass-spring problems because there is no initial velocity for the COM, the spring is at equilibrium, and the mass itself is the actuator of the force.

Questions:
1) How does adding the spring platform change x(t) for the COM?
2) Does the value for the spring constant K matter? (assume the spring obeys Hooke's law)
3) There should be an interplay between the leg force, the COM acceleration, and the spring compression (and expansion), but how is this represented in the differential equation?

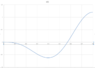
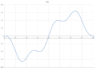
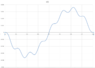
I tried to solve for x(t) using a second order ODE for a driven mass-spring system, and the result makes no sense. Therefore, I believe I set up the equation incorrectly. Could it be that the leg force is not "external" as in the usual mass-spring setup? If so, how do you work that into the equation?

 

[haruspex]

exerting a sinusoidal force

F=A sin(λx) or F=Asin(ωt)?

I tried to solve for x(t) using a second order ODE for a driven mass-spring system, and the result makes no sense.

Please post what you did.

 

[A.T.]

2) Does the value for the spring constant K matter? (assume the spring obeys Hooke's law)

If it wouldn't, then adding the spring in the first place wouldn't matter either.

 

[rcgldr]

Since a person doesn't have massless legs, switch the scenario to an ideal situation, no energy losses. Assume that spring constant is large enough that the same amount of internal work can be generated in the massless spring case as with the solid ground case. With this assumption, then the increase in gravitational potential energy (m g h) will be the same in either case. If the spring has losses and the same amount of work is input into the system, then the resulting height will be less in the spring case.

The advantage of a spring board or trampoline is when bouncing, where the same force can be applied over a longer distance than what is possible with a person's legs on solid ground.

 

[Bladerunner56]

thanks for the explanation.

 

[haruspex]

Assume that spring constant is large enough that the same amount of internal work can be generated in the massless spring case as with the solid ground case.

Not sure what you are saying there.
The main consequence of trying to do a standing jump from an initially stationary springboard is that you are likely to reach maximum leg extension when the board is below initial level, moving downwards, or both. That could seriously reduce the height achieved.
Certainly, as you say, there is no benefit from the board unless the legs are extended more than once.

It will require the actual equations (as requested in post #2) to solve it generally..

 

[Bladerunner56]

I approached this problem using the driven mass-spring equation:

$$m \frac {d^2 x} {d t^2} + c \frac {dx} {dt} + kx = F_0 \cos (\omega t + \phi)$$

The solution for x(t) is too long to write out here, but you can look it up, for example on hyperphysics. Using the general solution for x(t), I plugged in some values for the variables ($F_0 = 2000N, m = 65kg, \omega = 7.9rad/s, c = 0$ and the appropriate phase) and analyzed the motion over the first half period (0 to $\pi$) for different values of k. As suggested above, low values for k result in a longer period for the spring relative to the force period. When k is set to the resonant frequency, the spring returns to equilibrium as the force ends. And for high values of k, the spring exhibits complex harmonics. It would seem that the presence of a spring platform affects the jump height for values of k above and below resonance. Can this be correct? It would seem to violate conservation of energy. This function for x(t) assumes a point mass attached to the the spring, so the position x(t) is for the spring platform level. I realize it does not describe the position of the COM for the person jumping. Nevertheless, is it an appropriate function for the spring platform? Or is this the wrong diff. eqn due to the mass being the force actuator as opposed to the force being external?

 

[haruspex]

When I first read post #1 I took it to involve only a single extension of the legs. But now I am wondering if you chose sinusoidal force because you want to model the way is springboard is used in reality. If so, you need to arrange that the force is never attractive - the feet are not stuck to the board.
Assuming x=0 is the equilibrium position of the system, your F is relative to mg, but that still puts an upper limit of +mg for the upward force on the board.
Or maybe you are really thinking of a general damped forced oscillation, so the feet should be taken as stuck to the board?

 

[Bladerunner56]

Thanks for the clarifying questions. I want to model reality, where the board is not stuck to the feet. In Matlab, I attempted to model the limit to the leg extension (force never attractive) by using a window function to stop the force after once cycle. Then only gravity would be pushing on the mass after leg extension and with a high enough amplitude, you should be able to model lift-off. But the model shows the springboard oscillating at its natural frequency, which for high k, is higher than the force frequency. It seems that the platform height should move smoothly according to $F(t)_{net} = kx$, essentially following the net force by a factor k over that first cycle. Do the high frequency oscillations point to a problem in the equation setup?

 

[haruspex]

But the model shows the springboard oscillating at its natural frequency

The standard solution for forced-damped assumes it to have settled down to oscillate at the driving frequency.
Since you are only modelling for one oscillation of the driver you will need to allow for the transient solutions:
https://en.wikipedia.org/wiki/Harmonic_oscillator#Driven_harmonic_oscillators

 

[rcgldr]

Not sure what you are saying there. The main consequence of trying to do a standing jump from an initially stationary springboard is that you are likely to reach maximum leg extension when the board is below initial level, moving downwards, or both. That could seriously reduce the height achieved.

I was considering an ideal case where there are no losses in the system, that the person never separates from the "spring" during the sequence, a massless spring, and the same amount of internal potential energy converted into mechanical energy, which is eventually turned into gravitational potential energy at the peak height (with zero kinetic energy related to velocity). In this ideal spring case, it takes longer, but eventually the person reaches the same height as the ground case, with the ideal assumptions (no energy losses) that I made in my prior post.

Also as noted in my prior post, in a real world situation, losses in the spring (or springboard or trampoline) means the height will be lower for the same internal energy consumed versus the ground case (assuming there are no losses or less loss in the ground case).

 

[Bladerunner56]

Thank you. This all makes sense. It is interesting to look at the spring motion as $\omega_{spring} / \omega_{legs}$ gets larger than 1.0. These graphs of output show the harmonics I was referring to. $\omega_{spring}/\omega_{legs} = 1, 4, 8.$ Showing a half period. This solution includes the transient term. Would you only see this behavior with feet stuck to the spring board? If so, for feet not stuck, the mass-less spring board would simply follow the force impulse?

 

[Bladerunner56]

correction, full period (0.8).