- #1
iloveannaw
- 45
- 0
Homework Statement
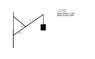
Please see attachment. A uniform massive beam attached to a wall at one end and supported by a cable (also attached to wall). On the free end of the beam is a weight. We are supposed to find the tension in the cable.
Homework Equations
sum of the torques about "pivot" (point where beam meets wall):
The Attempt at a Solution
where [tex]\alpha[/tex] is the given angle of 60° and [tex]\theta[/tex] is the angle of the beam to the horizontal. Also W is the weight of the load, WB anf F is the force in the supporting cable.
[tex]\Gamma = 0 = L_{1}Fsin \alpha - \frac{1}{2}(L_{1} + L_{2})W_{B}cos \theta - (L_{1} + L_{2})Wcos \theta[/tex]
[tex] L_{1}Fsin \alpha = \frac{1}{2}(L_{1} + L_{2})W_{B}cos \theta + (L_{1} + L_{2})Wcos \theta[/tex]
From there it should be a simpple step to solve for F. The problem is I can't work out [tex]\theta[/tex]. Is there a way using the information provided?
thanks