Statics: find zero-force members in frame

[SoylentBlue]

Homework Statement

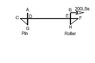
We are given this frame and asked to find the forces at C, D, E and F. Distance from D to E is 16 feet. Distance from C to D is 8 feet; distance from E to F is also 8 feet. Distance from A to D is 6 feet; distance from D to G also 6 feet.[/B]

Homework Equations

The Attempt at a Solution

We first look at the entire frame, and take the moment about G. This gives us Hy as 150; Gy must be -150 to balance the Y forces. This agrees with the book's answer.
Sum of x forces: Gx plus the 200LB force=0, so Gx = -200. Hx, because it is a roller, must be 0. This agrees with the book too.

OK. So far so good.

Now, why can't we make 2 immediate assumptions:
1) Assume Ax and Ay both are zero, since A is just sitting there with no forces on it.
2) Both C and F should be zero, since they are 2-member elbows with no external forces; aren't CD and EF classic examples of zero-force members?

I see that CG and HF are 2-force members under influence of G and H, respectively, but again this seems to directly contradict what we learned, when we looked at trusses, about how to spot zero-force members.
Thank you in advance for any help!
[/B]

 

[alw34]

I see that CG and HF are 2-force members under influence of G and H, respectively, but again this seems to directly contradict what we learned, when we looked at trusses, about how to spot zero-force members.

Since CF and other members are rigid, looks like CG and HF if removed, would not change the problem?? Agree or not?? If so, there are no forces there...

 

[SoylentBlue]

If CF and HG were removed, I would think the whole thing would just collapse; the 200LB force at B would swing the leg out at H, and BEH would rotate clockwise about E.
According to the book, here is the answer:
Cx= 200 <--
Cy=150 up
Dx=0
Dy=300 down
Ex = 400 -->
Ey=300 up
Fx = 200 <--
Fy = 150 down

I just don't see, working backwards and now knowing the answer, what the logic is. If we break the frame into its components (like we did in every previous problem; see exploded view), we have the 4 units consisting of GC, ADG, BEH and HF.

If we look at ADG for example, at point G it has a 200LB force going to the left and a 150LB force going down (we determined these values from looking at the entire frame, as outlined previously). If we assume Ax and Ay are zero, then only D is left to counter these forces. And that contradicts the book's answer.

OK, let's instead apply the 200LB and 150LB forces at G to CG, which is a simple 2-force member. Then Cx would be 200 --> and Cy would be 150 up. The book shows Cx going to the left, not right.

What am I missing here? (I should mention here that I am trying to work through this statics course alone, and that I am not registered for classes right now; I have only my textbook and the Internet to guide me.) Thank you again for any insights.

 

[alw34]

If CF and HG were removed, I would think the whole thing would just collapse;

possibly...depends...are they pinned or rigidly connected...

 

[SoylentBlue]

All the points are pinned. Since H is a roller, it cannot resist any horizontal force, so I would think the entire right side of the frame would collapse without HF to brace it.
So HF would have to be in tension.
Which brings me back to one of my initial questions: the book clearly states that joints like joint F (elbows that have no external forces; this qualifies) consist of zero-force members; yet logic dictates that HF would have to be in tension.

 

[PhanthomJay]

All the points are pinned. Since H is a roller, it cannot resist any horizontal force, so I would think the entire right side of the frame would collapse without HF to brace it.
So HF would have to be in tension.
Which brings me back to one of my initial questions: the book clearly states that joints like joint F (elbows that have no external forces; this qualifies) consist of zero-force members; yet logic dictates that HF would have to be in tension.

SoylentBlue
You are making some very good observations. The issue here is that the zero force member rule applies to pure trusses only, that is, only when the members are subject to axial tension or compression forces only. In your example, you don't have a pure truss, you have a frame, and in which case certain members may be subject not only to axial loads, but to shear loads and bending moments as well.
You have the support reactions. The Free Body Diagram is an engineers best friend. Try looking at the left side of the frame first with a free body diagram about ADGC that cuts through the horizontal member just through the right of D. There are now unknown axial and vertical shear loads, and a bending moment couple, in that horizontal member acting on joint D. Solve for them using the 3 equilibrium equations. Once you find them, you can now draw a free body diagram around ADG that cuts through the horizontal member on the right of D and the horizontal member to the left of D and the 2 force member CG. Solve for those member forces and moments.

 

[SoylentBlue]

Thank you for replying!
OK, so we have the left side of the frame, and we sum thusly:
Fx: -200 + Dx + Cx + Ax = 0
Fy: -150 + Dy + Cy + Ay = 0
Sum of moments around D: -(6)(200) -8Cy -6Ax = 0

Correct so far? Can't we assume that Ax and Ay are 0? A is a cantilever with no external forces.

For the moment about D we have 2 clockwise forces (Gx and Cy), with nothing to counter it...except at A, which seems counter-intuitive.

Again, thank you for your help.

 

[PhanthomJay]

Thank you for replying!

you are to be commended for attempting this problem without formal instruction: it is a bit tricky and I'm not sure I have it right.

OK, so we have the left side of the frame, and we sum thusly:
Fx: -200 + Dx + Cx + Ax = 0
Fy: -150 + Dy + Cy + Ay = 0
Sum of moments around D: -(6)(200) -8Cy -6Ax = 0

Correct so far?

in the free body diagram you have drawn, you must look at the externally applied forces and the internal forces/ moment that the cut horizontal member DE exerts on joint D. Since there are no external forces at C or A, and since you haven't made any cuts at C, there are no forces acting at C either, in this diagram. So adjust your equations to eliminate any C or A forces at this time. Also, when summing moments, there must be a moment (couple) in member DE.

Can't we assume that Ax and Ay are 0? A is a cantilever with no external forces.

that is correct , nothing going on there.

For the moment about D we have 2 clockwise forces (Gx and Cy), with nothing to counter it...except at A, which seems counter-intuitive.

it is counter intuitive , so firstly, get rid of the Cy term because there is no Cy in this particular diagram. Then the moment from the force Gx must be countered by the moment that exists in member DE.

Again, thank you for your help.

solve for the forces and moment in the member DE that are exerted on the joint. Then the next step is to look at another free body diagram to examine what is happening in the other members CD and CG. Note that Dx will not be zero at this time.

 

[SoylentBlue]

Before we go any further...just want to double-check: is the book's answer correct? It is internally consistent; all the x and y forces on CDEF total zero, and if you take a moment about C, D, E or F, the moments all balance. But that doesn't necessarily mean it is correct.

 

[PhanthomJay]

I get the same answers as the book. When they ask for the forces at D, E, etc., they mean to say " what are the forces acting on the pins at D, E, etc. ".

 

[SoylentBlue]

Thank you for pointing me in the right direction by mentioning that the answer shows the forces that the pins feel, not the forces that the pins must exert. So my confusion was, in part, a matter of nomenclature.

The book’s tactic, in every problem in this section, was this: first look at the frame as a whole, and determine as many pin/roller forces as you can. Then dismember it, and look at the forces on each individual member.


So that’s what I did.

And I now have 6 of the 8 forces solved. Here’s what I did.

I started with member BEH. This is simply 2 opposing lever arms and a fulcrum. The 200LB force is one lever arm, E is the fulcrum, and HF is the opposing lever arm. Because of the geometry (a 3/4/5 triangle), the tension in HF must be 250 to oppose the 200LB force at B.

Also, because of the geometry, the tension in HF induces a 150LB downward force.

So, Fx =200 to the left; Fy = 150LB down.

Fx=200 to left

Fy=150 down

This agrees with the book.

Back to BEH. The roller pushes up with 150LB; the tension in HF adds another 150LB. So E feels a 300LB force pushing up. It also feels 2 200LB forces pulling to the right, so Ey=400LB

Ex=400 to right

Ey=300 up

That agrees with the book too.


Awesome. We’re halfway there.

OK, over to the left side. Look at ADG. G has a 200LB force pulling to the left, and a 150LB force pulling down. Same geometry for CG (3/4/5 triangle), so the force of CG adds an additional 150LB pull down, for a total of 300 down.

Dy=300 down

CG is a 2-force member, so the resultant at C is a 150LB force up.

Cy is 150 up


My answers for Dy and Cy agree with the book.

We’re 75% of the way there.

And here’s where I’m stuck.

CG is a 2-force member, so the resultant at C should be a 200LB push to the right; we apply the same logic that we did to the right side.

Cx=200 to right (book says Cx goes to left)

Please help. I've spent a lot of time on this but I really want to understand the concept before I move on to the next topic in the book (this is one of the last problems in this section). Again, thank you for your assistance.

 

[PhanthomJay]

Very good. Firstly, however, the direction of the forces on a pin are largely a matter of convention. At joint F, for example, you note that the horiz force of HF is left, correct, but you could also say that the horiz force of EF on the pin at F is right ( it must be, for equilibrium). But let's stick with your convention and say that the force on F is left. You correctly note that FH is in tension, exerting a pulling force downward and leftward on F. Now let's move to C. Member CG is in compression, and as such, it is a pushing force acting upward and to the left on C. I think you may have been looking at the horizontal reaction force at G rather than the horizontal force in CG at G. Their directions are opposite.

If you agree, that's 7 out of 8. I see you saved the best for last: the mysterious x force acting on the pin at D.

 

[SoylentBlue]

Thank you for, ahem, pushing me in the right direction.
Little engineering joke there.
But I digress.
I should have been thinking like an engineer, and realized that these members can only be either in tension or compression.
And of course, because G is pushing to the left, that is forcing CG into compression.
So C feels a compressive force, and that force is pushing it to the left, which agrees with the book.
Now on to the last force: D in the x direction.
The only way I can see to reconcile the Dx force is to include the 400LB pull on D from E. Then the 200LB leftward pull at C, and the 200LB leftward pull at G balance out the 400LB rightward pull from E.

What was initially throwing me was when I was examining the forces at C: I saw a 200LB pull to the left causing compression of CG, but also saw a 150LB pull down at G, which I thought should conversely lead to tension in CG.

BTW, thank you for the encouragement. I am trying to do this on my own, part-time, squeezing in studying along with a full-time job. So a little encouragement goes a long way.

 

[PhanthomJay]

Thank you for, ahem, pushing me in the right direction.
Little engineering joke there.
But I digress.
I should have been thinking like an engineer, and realized that these members can only be either in tension or compression.
And of course, because G is pushing to the left, that is forcing CG into compression.
So C feels a compressive force, and that force is pushing it to the left, which agrees with the book.
Now on to the last force: D in the x direction.
The only way I can see to reconcile the Dx force is to include the 400LB pull on D from E. Then the 200LB leftward pull at C, and the 200LB leftward pull at G balance out the 400LB rightward pull from E.

What was initially throwing me was when I was examining the forces at C: I saw a 200LB pull to the left causing compression of CG, but also saw a 150LB pull down at G, which I thought should conversely lead to tension in CG.

BTW, thank you for the encouragement. I am trying to do this on my own, part-time, squeezing in studying along with a full-time job. So a little encouragement goes a long way.

This problem must have been for "extra credit", because it goes well beyond the intro level. Without the answer key, it is not easy to establish the pin forces, especially to establish that there is no horizontal force on the pin at D. Once again, you are to be highly commended for your effort.