Statics problem (moment and equilibrium)

[bardia sepehrnia]

1. Having really hard time understanding the concept of moment and equilibrium in statics. In the following picture the man is carrying a 6kg uniform rigid board. I'm asked to calculate the amount of force the man feels on his shoulder. (at point A)

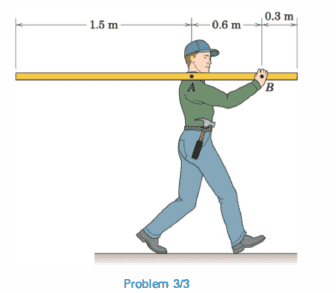
Now I know I'm supposed to start by making a free body diagram, but I don't know where would the weight of the board be placed. Is it in center of the board regardless of the support point at A, or do I have to separate the weight into 2 components based on its length, one in front of the man and one behind him?

 

[berkeman]

Welcome to the PF.

The worker is having to pull down at point B in order to balance the board on their shoulder. Where is the center of mass of the board? How do the force down at B and the force up at A keep the board from falling or turning?

Please take a try at the FBD so we can work from there. Thanks.

 

[bardia sepehrnia]

Welcome to the PF.

The worker is having to pull down at point B in order to balance the board on their shoulder. Where is the center of mass of the board? How do the force down at B and the force up at A keep the board from falling or turning?

Please take a try at the FBD so we can work from there. Thanks.

I think I figured it out but I'm not sure.

So ∑M=(W₁×(1.5/2))-(W₂×(0.9/2)-(0.6B)=0
Then by calculating Force at point B and adding it to the total weight, the total force on the worker shoulder is calculated?

 

[berkeman]

The total free weight should be acting down at the center of mass -- I'm not able to tell if that's what you are doing yet from your FBD...

 

[bardia sepehrnia]

The total free weight should be acting down at the center of mass -- I'm not able to tell if that's what you are doing yet from your FBD...

I separated the weight:into 2 components. But I also used your method and got the same answer! So I calculated the moment using point A as reference based on your method:
W=6×9.81=58.86 and the weight force is acting at 1.2 meter from the edge or 0.3 meter from worker's shoulder (1.2-0.9=0.3)
Then ΣM=Rd so ΣM= (58.86×0.3) - (0.6B) = 0 ⇒ B= 17.658/0.6 = 29.43
Force on worker's shoulder is then W+B = 58.86 + 29.43 = 88.29

 

[berkeman]

Looks reasonable. Be sure to include units in all of your calculations. What are the units of Force or Weight?

 

[bardia sepehrnia]

It's Newton (N) :)