mhrob24
- 53
- 9
- Homework Statement
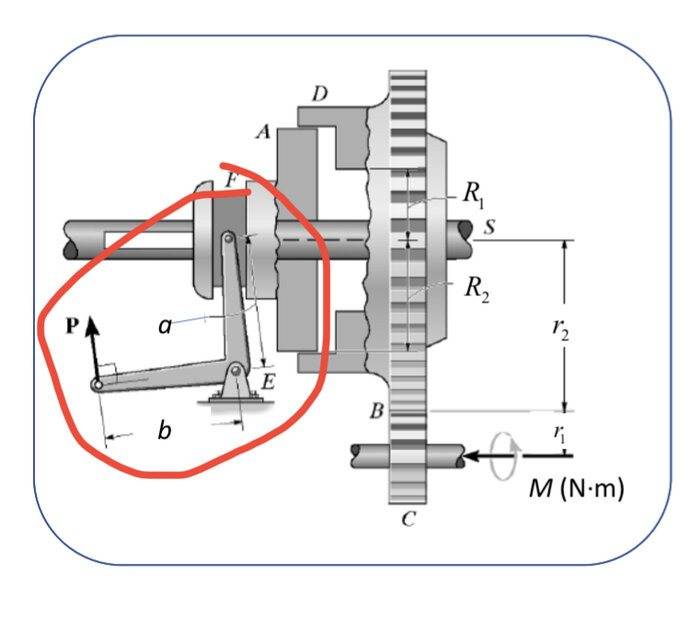
- Determine internal loads (shear and moment) of the control arm and draw the corresponding diagrams.
- Relevant Equations
- M = Fd = 0
Fy = 0
Part of a project I am working on (part #3…see description below) is asking us to find the internal loads (shear and moment) and draw the corresponding shear/moment diagrams of the control arm shown below. It’s a little tricky to me, because all of the members associated with these type of problems are normally straight….this travels along the x and y (it’s bent…)
The FBD I drew below shows how I THINK this should be sectioned in order to create the moment and shear diagram, but I’m really not sure. The moments do cancel when you reach the end of that member along the x-axis, so it seems like this should be accurate. Any insight would be beneficial. Thank you!

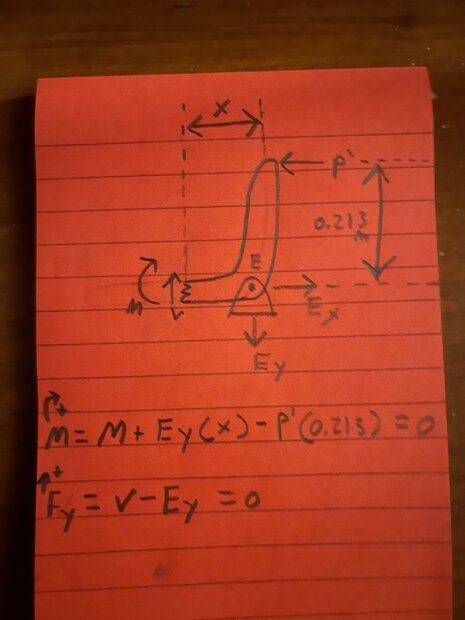
The FBD I drew below shows how I THINK this should be sectioned in order to create the moment and shear diagram, but I’m really not sure. The moments do cancel when you reach the end of that member along the x-axis, so it seems like this should be accurate. Any insight would be beneficial. Thank you!