Discussion Overview
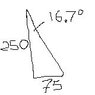
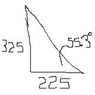
The discussion revolves around a statics problem involving two blocks (20KG and 10KG) being pushed against a wall with friction. Participants are attempting to determine the smallest force P required to prevent slipping, while navigating through the complexities of forces, normal forces, and torques involved in the system.
Discussion Character
- Homework-related
- Mathematical reasoning
- Technical explanation
- Debate/contested
Main Points Raised
- The initial setup involves calculating forces in both x and y directions for the 10KG and 20KG blocks, considering the coefficient of friction.
- Some participants suggest starting with free body diagrams (FBDs) to visualize the forces acting on the blocks.
- One participant proposes that the force of tension applied by the rods could be useful in determining the vertical forces acting on the 10KG block.
- There is a discussion about the influence of the 10KG block on the 20KG block, particularly regarding how friction affects their interactions.
- Multiple participants recommend creating FBDs for the entire system rather than individual blocks to simplify the analysis of forces and torques.
- Equations for the sum of forces in both x and y directions, as well as for torques, are derived, leading to relationships between normal forces.
- One participant expresses uncertainty about including certain forces in the torque calculations and whether their logic is correct.
- A participant calculates a negative value for P, questioning whether a math or logic error occurred, especially in light of a conflicting answer from a textbook.
Areas of Agreement / Disagreement
Participants generally agree on the need for free body diagrams and the importance of considering all forces and torques. However, there is disagreement regarding the correct approach to the problem, particularly in how to account for the interactions between the blocks and the resulting calculations. The discussion remains unresolved as participants explore different methods and calculations.
Contextual Notes
There are limitations in the assumptions made regarding the forces acting on the blocks, particularly the influence of friction and the geometry of the system. Some participants express uncertainty about the correct application of torque calculations and the relationships between normal forces.