- #1
BryMan92
- 18
- 0
Homework Statement
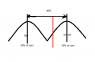
I am analyzing fuel economy of vehicles in Europe. Since there are gasoline (lower MPG) and diesel (higher MPG) I assumed the distribution to be bimodal. I am trying to deconstruct the data into a gasoline MPG and a diesel MPG. I have attached an image to explain my approach.
2. The attempt at a solution
I'm no statistician, so forgive me while I break math. I figured I could treat this system like balancing a lever on a fulcrum. Essentially, I said a diesel vehicle is 40% more than a petrol vehicle and the red line is a given average of the MPGs. So, I did the following maths:
% of Cars for Petrol * x = % of Diesel* (1-x)
x=7/10, x'=3/10
So, I said the gasoline vehicles would receive a 70% (the distance) *40% (difference in fuel economy) reduction, or (1-.7*.4)(Average), while diesel would receive a (1+30%*40%)(Average). Would this, by any chance, work or be accurate??
Thanks guys!