- #1
diy-er
- 14
- 2
- TL;DR Summary
- vertical square steel tube construction load
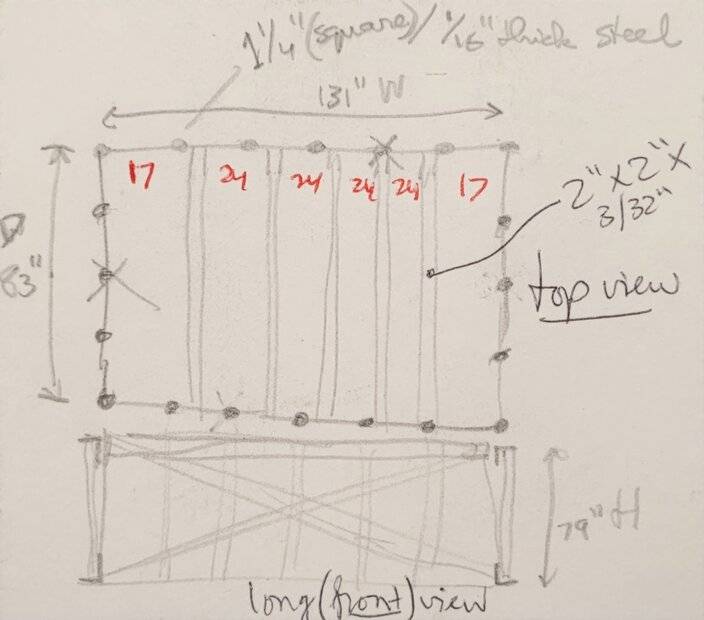
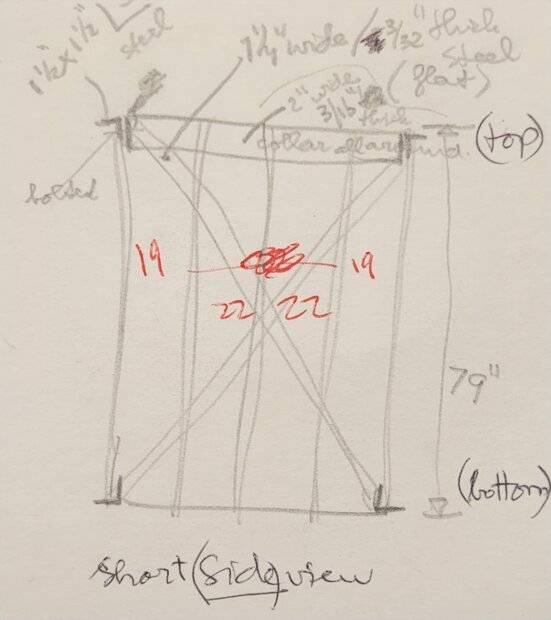
I have a VERTICAL standing square tube 1.25" x 1.25" x 1/16" thick.
Length/Height = 79"
Material = steel
How do you determine its max load capacity for this tube when mounted vertically?
I plan to use 18 of these vertical posts, evenly spaced, creating an 83" x 131" rectangular structure.
They will be welded together on the top, as well as on the bottom, by 2" steel L-bars (3/16" thick), 4 pieces of 83" length, and 4 are 131" long.
Next I will weld a cross (on all 4 sides for structural integrity), made with steel flat bars of 1.25" x 3/32" thick.
Finally it will have the top connecting the long sides, with 5 horizontally mounted, evenly spaced 2" x 2" x 3/32" square steel tubes.
My question is what the load capacity is per post, per square foot, and/or for the entire stucture.
Thank you
Length/Height = 79"
Material = steel
How do you determine its max load capacity for this tube when mounted vertically?
I plan to use 18 of these vertical posts, evenly spaced, creating an 83" x 131" rectangular structure.
They will be welded together on the top, as well as on the bottom, by 2" steel L-bars (3/16" thick), 4 pieces of 83" length, and 4 are 131" long.
Next I will weld a cross (on all 4 sides for structural integrity), made with steel flat bars of 1.25" x 3/32" thick.
Finally it will have the top connecting the long sides, with 5 horizontally mounted, evenly spaced 2" x 2" x 3/32" square steel tubes.
My question is what the load capacity is per post, per square foot, and/or for the entire stucture.
Thank you

