- #1
hjelmgart
- 127
- 17
Hi, last semester I did a project with two fellow students. We made a numerical model to calculate the reflectance from a periodic V-shaped structure of silicon similar to this:

In the course of doing so, we came across something we could not explain. I have placed an image of it below:
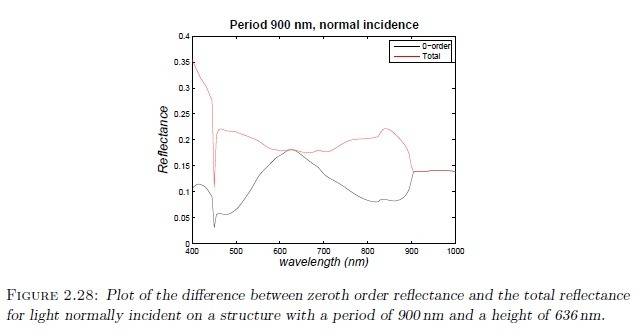
What you should notice, is that at a specific point it is only the 0'th order reflectance, which propagates. The wavelength at this point matches exactly the height of the structure. We saw this for any structure we modeled no matter the height.
Our model was quite good as our professor assisted us a lot with it, so we have no reason to doubt our results, and they were in good agreement with our measurements, so no problems there.
So far nobody at the university was able to explain this phenomenon, so now I am trying here, to see if someone might know of it or possibly have an idea, of how it could be explained?
The model was made for a period structure, which was infinitely deep (so that no light could be reflected from the bottom of the structure). In general it gave a realistic view of how these V-shaped grooves could reduce the reflectance from the surface of a silicon wafer.
In the course of doing so, we came across something we could not explain. I have placed an image of it below:
What you should notice, is that at a specific point it is only the 0'th order reflectance, which propagates. The wavelength at this point matches exactly the height of the structure. We saw this for any structure we modeled no matter the height.
Our model was quite good as our professor assisted us a lot with it, so we have no reason to doubt our results, and they were in good agreement with our measurements, so no problems there.
So far nobody at the university was able to explain this phenomenon, so now I am trying here, to see if someone might know of it or possibly have an idea, of how it could be explained?
The model was made for a period structure, which was infinitely deep (so that no light could be reflected from the bottom of the structure). In general it gave a realistic view of how these V-shaped grooves could reduce the reflectance from the surface of a silicon wafer.
Last edited: