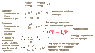Since EM has been mentioned in this thread let's see just what's really going on at a slightly non-rigorous level, but somewhat above B level. Have a look at good old F=ma. We will generalize this a bit to get something I call J and have it equal to k(d^2/dt^2)A where k is some constant and like J will not say anything yet about A. Now we will assume something about J - it is a 4 vector so you get Ju = k (d^2/dt^2) Au. This does not conform to the requirement of relativity - it should have the same form in all frames - the means (d^2/dt^2) should be ∂v∂v (of course the v should be raised in the second ∂v but I dot want to go to the trouble of Latex). The equation then is Ju = k ∂v∂v Au. We will assume Ju whatever it is is conserved ie obeys the equation of continuity ∂uJu = 0. This means ∂v∂v∂μAu = 0. To make this always true we will take ∂μAu = 0. The is called the Lorentz Gauge condition. Au is called the vector potential and Ju is called the 4 current. These are Maxwell's equations in the so called Lorentz gauge - given special relativity they are not hard to come up with.
K simply determines units so we will take it as 1 for simplicity.
The equations then becomes ∂u∂u Av - ∂u∂vAv = Jv (1) since ∂vAv = 0.
Take this equation and we notice something. If we substitute A'v = Av + ∂vΛ, where Λ is any function of the xi, for Av then we get exactly the same equation in A'v. In fact if we take ∂v∂vΛ= -∂vAv we have a differential equation in Λ, solve it for Λ, and you then get the Lorentz Gauge condition. Take (1) as our equation and we see it has this very interesting gauge symmetry. Its an example of what's called U(1) symmetry. I am not 100% who exactly showed this symmetry is in fact the rock bottom essence of EM - it may be Weyl or Schwinger or someone else - but physicists now know its really the essence of Maxwell's Equations.
What I wrote is in some sense a derivation, but its validity depends on what went into it. It really is just fooling around with equations and seeing what you get - Dirac did this sort of thing a lot. Mostly it leads nowhere - but sometimes its reveals something quite interesting like here.
Now how do we get the usual form of Maxwell's equations.
Simply define Fuv = ∂uAv - ∂vAu and you get the normal electric and magnetic fields:
https://quantummechanics.ucsd.edu/ph130a/130_notes/node451.html
Forget the C; we will, for simplicity work in units C=1.
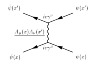
We have ∂v∂u Fuv = 0 as can be easily seen. And ∂uFuv = Jv so, as we assumed ∂vJv =0 ie the 4 current is conserved. This is how the field equations are arrived at but how do charged particles move? For this we use Lagrangian Field Theory. Lagrangian's take the form of Lp + Li + Lf. Here Lf is the Lagrangian of the field. Li is the Lagrangian of interaction between the field and charged particle and Lp is the Lagrangian of a particle. We have the equation of the EM field - that's the equation when you have no charge - just the field and it gives ∂uFuv = 0. To get Jv we have the interaction term which must be -JvAv. You add that to the particle Lagrangian and you get how a charged particle moves ie the Lorentz Force law. The gory detail can be found here:
http://www.phys.ufl.edu/~pjh/teaching/phy4605/notes/chargelagrangiannotes.pdf
This is a beginner thread, and what I wrote is at least I level. Don't be worried if its above your level - that's not why I posted it. It was simply to show there is no mystery in Electromagnetism - it is so well understood you can almost pull it out of nothing.
What string theory deals with are not issues like why we have negative charge - that isn't really a worry - string theory deals with much deeper issues - such as quantum gravity or like was mentioned before - suggesting that we have a massive number of spaces string theory can be compacted into. We live in a world that simply has one - we have to have one - the exact one we got isn't important as far as explanation is concercerned.
Thanks
Bill