- #1
Johnls
- 11
- 0
Suppose there are two vessels filled with water up to the same height:
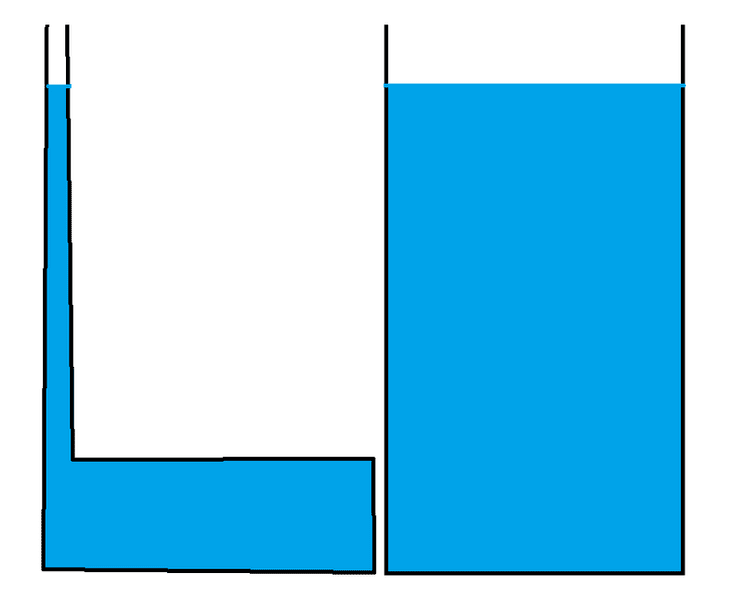
If I understand pascal's principle, the pressure in the bottom of both vessels should be the same. But the right one has more weight, so isn't the force on the bottom greater and therefore there is more pressure there?
If I understand pascal's principle, the pressure in the bottom of both vessels should be the same. But the right one has more weight, so isn't the force on the bottom greater and therefore there is more pressure there?