lektor
- 56
- 0
A radio wave undergoes a phase shift of 180 degrees when it reflects from the calm surface of the ocean. In early days of radioastronomy, Australian Astronomers observed the interference between a radio wave arriving at the their antena on a direct path from the sun and on a path involving one reflecting on the sea surface. If their antenna was located on the coastline 25m above the sea level and the radio waves had a frequency of 60 MHZ, find the least angle above the horizon for the sun that results in destructive interference of the waves at the receivng antenna.
The identity cos 2θ = 1-2sin^2θ
Ok, so that is the problem right now i have a diagram and understand destructive interference will occur when (n - 1/2 )λ
Wavelength in this situation is
V = Fλ
therefore λ = 60x10^6 / c
λ = 5m
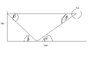
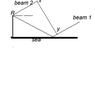
the attachment is of my current diagram ( sorry for the crude drawings, only had paint avalible).
Cheers.
The identity cos 2θ = 1-2sin^2θ
Ok, so that is the problem right now i have a diagram and understand destructive interference will occur when (n - 1/2 )λ
Wavelength in this situation is
V = Fλ
therefore λ = 60x10^6 / c
λ = 5m
the attachment is of my current diagram ( sorry for the crude drawings, only had paint avalible).
Cheers.