Supercapacitor dragster project

[Fred404]

Hi all!

I’m currently working on a project for which students will have to build a supercapacitor based dragster.

I saw here and there some videos on how it works but it’s too general to give me hints about components choice. So here I am with my questions, hoping that I’ll get enough answers to go forward with this project ;)

So, here it is:

I want students to build a small dragster (basically very light, made of wood sticks and such, not a big thing!) to organize a contest (drag race) on very small distance (let say about 3 meters max).

As for any school project, the amount of money is limited! No way to build a drag for 50$ each unfortunately.

Here are the components I was thinking about:

A small dc motor Gikfun DC 3V-6V Motor 2000 RPM

Here are specs:

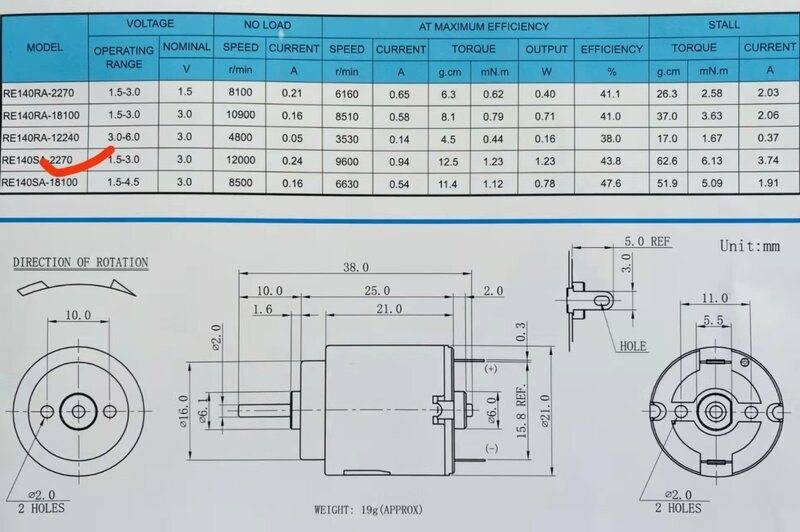
I was planning to feed it up with supercapacitors only. I was thinking of supercapacitor 2.7V, 10F to build a power pack in parallel if needed.

Here is what I’ve done so far (if I’m not wrong):

Energy stored in the supercapacitor 2.7V/10F

E=1/2.C.U2

E = (1/2)* 10F * 2.72²V

E= 36.45 JoulesResistance of the DC motor:

R = U/I

At Maximum Efficiency – according to specs – we have 0.94A for 3V

R = 3V/0.9A = 3.34 ohm
Time of charge tho (sorry, don’t know the translation in English) for this setting:

Tho = R . C = 3.34 ohm x 10F = 33.4 s
So, this means that if tho = 33.4s, after 33.4s, there will only 37% energy left in capacitor.

After 5x tho, the capacitor will be empty.
Energy required for the race:

This is where I think, calculation may be inaccurate cause it depends on the weight of car (the heavier, the more energy needed)

Let say the car is about 150g (0.15 Kg)

F = m x g
F = 0.15 x 9.81 = 1.47 N

For a 3 meters race:

W = F x d
W = 1.47 x 3 = 4.41 J

For the motor, at Max Efficiency, we have 0.94A at 3V (even though the supercapacitor will only deliver 2.7V) for a 5 sec race

P = UI and E = Pt
P = 3 x 0.94 = 2.82W
E = 2.82 x 5 = 14.1 Joules

So, all "energy needed together", this represents an overall total of 4.41 + 14.1 = 18.51 J

According to that, this means that 1 supercapacitor would be enough
But just to have "backup", I can add an extra capacitor in parallel, which should give me twice energy...

So, am I totaly out of field? Does it make sens?

Also, does someone knows if I can buy a device to charge supercapacitors? I've found a diy to build one but it may take too much time for students to build it! So I was wondering if I could find a device that would do the job so that would just have to go to a station to charge their drag!

Thanks for any inputs ;)

Fred

 

[berkeman]

I haven't used supercaps much, but my impression is that they are for low output currents (like real time clock backup), not for high energy applications. I could be wrong about that though. Have you looked in detail at the supercap datasheet to see what it shows for maximum output current?

 

[jack action]

F = m x g

No. The force will be the wheel torque divided by the wheel radius, but can never exceed the tire friction force which is the tire-road friction coefficient times the vertical force acting on the driven wheel. (More info here and here.)

So, all "energy needed together", this represents an overall total of 4.41 + 14.1 = 18.51 J

No. The energy needed will be the calculated output energy (4.41 J in the example) divided by the motor efficiency (43.8 % from the chart given), thus 4.41 / 0.438 = 10.14 J.

 

[Fred404]

Thanks for those inputs: I'll check closer for both!
I haven't checked the datasheet for capacitors since I didn't ordered them yet and just check what is avail!