Surface Charge Density of a Neutral Conducting Cube

[inevitable08]

Homework Statement

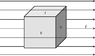
There is a region of space containing a uniform electric field of strength E. A neutral conducting cube with side length s is placed into this field. The cube is aligned with the field. You may assume that the electric field outside the cube is unaffected by any changes that occur in the cube. Use Gauss’ Law and your knowledge of conductors to find the surface charge density, if any, on each face of the cube. Your results may be in terms of E, s, and any appropriate constants. The three visible cube faces are numbered, I, II, and III. Assume that face IV is opposite face I, face V is opposite face II, and face VI is opposite face II.

Homework Equations

Electric Flux = E (dot) A = EAcosθ = Q_encl/\epsilon_{o}\
η = surface charge density of a plane of charge = q/area

The Attempt at a Solution

Ok since we are dealing with a cube this means the surface is flat and the charge density is not changing so we don't need to integrate A for surface. I also know that any area vectors of the cube that are orthogonal with the electric field creates an electric flux of 0. This means sides I, II, IV, and V are all going to be 0 this now leaves us with III and VI.

III's area vector is in same direction as the field so this means cos(θ) = 1 and VI is opposite and cos(θ) = -1.

A(q/A) = Aη = Q_encl

plug in information

EA = Q_encl/\epsilon_{o}\

EA = Aη/\epsilon_{o}\

E\epsilon_{o}\ = η


-------------------------------------------------
I just feel this can't be right, seems to simple

 

[ehild]

It is inevitably correct.

ehild