themagiciant95
- 56
- 5
If i want to calculate the volume of a cone i can integrate infinitesimal disks on the height h of the cone.
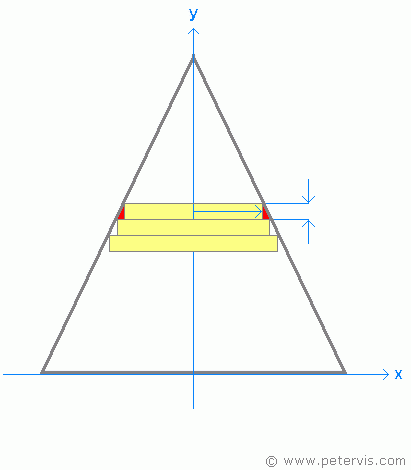

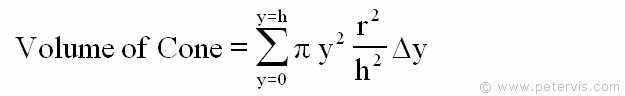
I was told that if i want to calculate the surface of the cone, this approximation is not correct and i have to take the slanting into account, this means that instead of infinitesimal disk i have to consider infinitesimal conical frustum and integrate the lateral surface of each infinitesimal conical frustum. Why for the surface i can't use infinitesimal disks as for the volume calculation ?
Furthermore, the formula for the lateral surface of a conical frustum is :
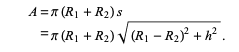
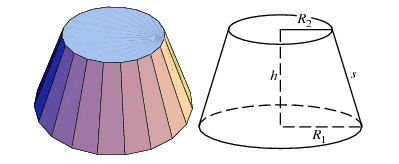
Now, let's consider an infinitesimal conical frustum.
For h\rightarrow 0 , R_{1}\approx R_{2} so (R_{1} - R_{2})^{2} \rightarrow 0 and the surface of an infinitesimal conical frustum would be2\pi R_{2}\,dh, however i was told that it's not correct. The correct one is 2\pi R_{2}\sqrt{ d(R_{2}-R_{1})^{2}+ dh^2}, why?
I was told that if i want to calculate the surface of the cone, this approximation is not correct and i have to take the slanting into account, this means that instead of infinitesimal disk i have to consider infinitesimal conical frustum and integrate the lateral surface of each infinitesimal conical frustum. Why for the surface i can't use infinitesimal disks as for the volume calculation ?
Furthermore, the formula for the lateral surface of a conical frustum is :
Now, let's consider an infinitesimal conical frustum.
For h\rightarrow 0 , R_{1}\approx R_{2} so (R_{1} - R_{2})^{2} \rightarrow 0 and the surface of an infinitesimal conical frustum would be2\pi R_{2}\,dh, however i was told that it's not correct. The correct one is 2\pi R_{2}\sqrt{ d(R_{2}-R_{1})^{2}+ dh^2}, why?