peripatein
- 868
- 0
Hi,
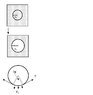
A square frame with a thin crust/layer of liquid with surface tension γ is given. Into the plane of the frame an elastic wire of circular shape with radius r_0 is inserted. The thin crust/layer of liquid is then burst (by pricking) and as a result of the force of the surface tension exerted on the wire, the elastic wire extends and rapidly attains a new radius, r_1.
It is also given that the tension in the wire is proportional to the lengthening of the wire wrt its flaccid length, with a constant k.
I was asked to find an expression for the surface tension (γ) of the liquid, using k, r_1, and r_0.
The question advises to use the diagram in the attachment.
So I wrote down the following equation: 2Tsine(phi) = 2γdl
And T = k(l_1-l_0) = 2pi*k(r_1-r_0)
Hence, pi*k(r_1-r_0) = γ
I am not sure these equations are correct. May you kindly advise?
Homework Statement
A square frame with a thin crust/layer of liquid with surface tension γ is given. Into the plane of the frame an elastic wire of circular shape with radius r_0 is inserted. The thin crust/layer of liquid is then burst (by pricking) and as a result of the force of the surface tension exerted on the wire, the elastic wire extends and rapidly attains a new radius, r_1.
It is also given that the tension in the wire is proportional to the lengthening of the wire wrt its flaccid length, with a constant k.
I was asked to find an expression for the surface tension (γ) of the liquid, using k, r_1, and r_0.
Homework Equations
The Attempt at a Solution
The question advises to use the diagram in the attachment.
So I wrote down the following equation: 2Tsine(phi) = 2γdl
And T = k(l_1-l_0) = 2pi*k(r_1-r_0)
Hence, pi*k(r_1-r_0) = γ
I am not sure these equations are correct. May you kindly advise?